24  Bivariate EDA

Exploratory Data Analysis of the Relationships between Pairs of Variables

Bivariate Exploratory Data Analysis (EDA) moves beyond examining variables individually, instead focusing on relationships between two variables. In business analytics, understanding how variables interact is essential for revealing patterns, trends, and insights that a single-variable analysis cannot provide. For entrepreneurs, bivariate analysis opens the door to understanding how key factors such as price and demand, or marketing spend and sales, influence one another—insights that are critical for making data-informed strategic decisions.


24.1 Why Bivariate Analysis Matters

Exploring relationships between two variables allows us to:

  • Discover Associations: Identifying connections between variables helps uncover meaningful patterns. For example, understanding how customer age correlates with spending levels can reveal age groups that are more likely to make high-value purchases, informing marketing or product strategies.

  • Detect Trends: Observing trends, such as how marketing spend relates to sales growth, enables businesses to make proactive decisions. For instance, discovering that increased advertising spend drives up sales during certain seasons can guide budget allocations.

  • Inform Predictive Modeling: Bivariate analysis provides the foundation for more advanced analytics, allowing for predictive insights that drive business growth. Recognizing that price fluctuations correlate with demand changes, for example, can help entrepreneurs adjust pricing strategies to maximize sales and customer satisfaction.

By mastering bivariate techniques, you’ll gain the skills to uncover valuable insights that arise when two variables interact, enhancing your ability to make data-driven decisions in entrepreneurship.

Key Learning Objectives

  • Explore two-variable relationships to identify trends, associations, and insights in business analytics.
  • Use bivariate techniques to understand and interpret how variables interact in real-world business contexts.
  • Apply fundamental bivariate methods in R, including descriptive statistics and visualizations, to uncover relationships between variables.
Entrepreneurial Insight

Observing relationships, like the link between marketing spend and sales, allows you to allocate resources more effectively and tailor strategies to maximize impact. Spotting associations between customer demographics and buying behavior can also help you optimize your product offerings and target your audience more precisely.

In the following sections, we’ll explore bivariate analysis techniques, using data from UrbanFind to demonstrate how examining relationships between variables can unlock valuable insights for entrepreneurs.


24.2 Numeric-Numeric Analysis

When analyzing two continuous variables, it’s essential to understand how they interact. Numeric-numeric analysis focuses on the relationship between pairs of numeric variables, helping us identify if and how one variable might change in response to changes in another.

In this section, we’ll explore covariance and correlation to quantify these relationships and learn how to visualize them effectively using scatter plots with trend lines.

Covariance and Correlation

In bivariate analysis, understanding the covariance and correlation between two variables is essential to assess the nature and strength of their relationship.

Covariance

Covariance provides a measure of how two variables move together. A positive covariance suggests that as one variable increases, the other tends to increase as well. Conversely, a negative covariance indicates that as one variable increases, the other tends to decrease. If the covariance is close to zero, it suggests that the variables do not have a consistent pattern of movement together.

To make this clearer, let’s look at three simple examples that represent positive, negative, and near-zero covariance.

Figure 24.1: A bivariate relationship between continuous variables may have postive, negative, or zero covariance.

In these plots:

  1. Positive Covariance: Points move in an upward direction together, indicating that as x increases, y tends to increase.
  2. Negative Covariance: As x increases, y tends to decrease, producing a downward trend.
  3. Near-Zero Covariance: There’s no consistent pattern between x and y, indicating a weak or nonexistent relationship.

Correlation: Pearson vs. Spearman

Correlation provides a standardized measure of how closely two variables move together, making it easier to interpret relationships on a consistent scale.

  • Pearson Correlation: Measures the strength and direction of a linear relationship between two variables. It assumes that both variables are normally distributed and linearly related. Pearson correlation values range from -1 (perfect negative linear correlation) to +1 (perfect positive linear correlation), with 0 indicating no linear relationship.
  • Spearman Correlation: Measures the strength and direction of a monotonic relationship,1 based on ranks rather than actual values. It’s useful when data doesn’t meet the assumptions of normality or linearity, as it captures relationships that are not strictly linear.

Recall that we introduced UrbanFind’s customer_data in Chapter 23.2. UrbanFind is a startup specializing in curated recommendations for city dwellers in areas like tech, fashion, outdoor activities, and health. Here’s a quick reminder of the data structure and key variables.

# Display dataset structure
glimpse(customer_data)
Rows: 100
Columns: 4
$ age              <dbl> 33, 18, 32, 30, 85, 35, 31, 14, 24, NA, 37, 40, 52, 4…
$ spending         <dbl> 495, 458, 491, 420, 664, 533, 526, 350, 471, 424, 464…
$ product_interest <chr> "Fashion", "Fashion", "Health", "Fashion", "Fashion",…
$ region           <chr> "East", "North", "South", "South", "East", "East", "S…
  • Age: The customer’s age in years.
  • Spending: Monthly spending in dollars on lifestyle products, including tech, health, and outdoor gear.
  • Product Interest: The product category each customer is most interested in (Tech, Fashion, Outdoors, or Health).
  • Region: The geographic region (North, South, East, or West) where each customer resides.

This dataset helps UrbanFind understand the demographics, spending patterns, and interests of its audience. In this chapter, we’ll examine relationships between these variables, focusing on insights into customer behavior through bivariate analysis.

With this quick reminder of the data structure and key variables, let’s now explore both Pearson and Spearman correlations between age and spending to better understand customer behavior in the UrbanFind dataset.

Figure 24.2: A side-by-side visual comparison of Pearson (linear fit) and Spearman (rank-based fit) correlation.

In these plots:

  • Pearson Correlation (Linear Fit): A linear trend line is used to show how spending changes with age if we assume a linear relationship. Pearson correlation measures the strength of this linear relationship, which can help identify trends when variables have a straightforward increase or decrease together.
  • Spearman Correlation (Rank-Based Fit): A smoother line (using loess method) captures any monotonic (rank-based) association that doesn’t need to be linear. This plot shows how well the ranks of age and spending align, which is useful when relationships are not perfectly linear.

Demonstration: Calculating Covariance and Correlation

Covariance between age and spending

The following code explores the covariance between age and spending in UrbanFind’s customer_data.

# Compute covariance between age and spending
cov(customer_data$age, customer_data$spending, use = "complete.obs")
[1] -98.72329

Covariance between age and spending in the UrbanFind dataset is calculated as -98.7233. Covariance can be a bit tricky to interpret directly because it’s measured in combined units—in this case, years multiplied by dollars (since age is in years and spending is in dollars).

So, what does this value mean?

  • Negative Covariance: The negative value tells us that as age increases, spending tends to decrease. In other words, older customers in this dataset generally spend less. However, this number doesn’t tell us how strong the relationship is on its own.

  • Understanding the Magnitude: The size, or magnitude, of the covariance depends heavily on the units and scales of the variables. Because it combines units (like years and dollars), a covariance value of -98.7233 isn’t easily interpretable on its own—it’s hard to say exactly what this number means without comparing it to another dataset or variable on the same scale.

  • When to Use Covariance: Covariance is mainly useful for determining the direction of the relationship (positive or negative). To understand how strong the relationship is, we usually turn to correlation, which adjusts the values to fit within a range of -1 to 1, making it easier to interpret and compare across different variables.

In summary, this negative covariance value tells us that there’s a tendency for spending to decrease with increasing age in UrbanFind’s data. However, for a clearer sense of the strength of this relationship, correlation is often more helpful.

Pearson and Spearman Correlation between age and spending

To better understand the strength of the relationship between age and spending in UrbanFind’s customer_data, let’s calculate their correlation with the Pearson and Spearman methods. Notice the differences between the results: Pearson assesses linear relationships, while Spearman is more robust for non-linear relationships.

# Compute Pearson correlation between age and spending
cor(customer_data$age, customer_data$spending, use = "complete.obs", method = "pearson")
[1] -0.03552235
# Compute Spearman correlation between age and spending
cor(customer_data$age, customer_data$spending, use = "complete.obs", method = "spearman")
[1] -0.1056287

The correlation calculations between age and spending in the UrbanFind dataset yield the following results:

  • Pearson Correlation: -0.0355
  • Spearman Correlation: -0.1056

Interpretation

  1. Direction of Relationship: Both correlation values are negative, which indicates a slight tendency for spending to decrease as age increases. However, because these values are close to zero, the relationship is quite weak.

  2. Strength of Relationship:

  • The Spearman correlation is -0.0355, which suggests a weak, negative monotonic relationship between age and spending. This implies that there’s a slight general trend of decreasing spending with increasing age, but it’s not a strong or consistent pattern.
  • The Pearson correlation is even closer to zero at -0.1056, indicating that there’s almost no linear relationship between age and spending.
  1. Why Both Correlations?
  • Pearson correlation assesses linear relationships and is most informative when both variables follow a roughly normal distribution. Since the result is near zero, it suggests there’s little to no linear relationship between age and spending.
  • Spearman correlation focuses on rank-based (monotonic) relationships, which don’t have to be linear. This value is slightly larger in magnitude, suggesting there’s a very weak tendency for older customers to spend less, though it’s not strong enough to be meaningful.

In practical terms, these correlations indicate that there’s minimal relationship between age and spending in the UrbanFind data. Although older customers might spend slightly less on average, the relationship is too weak to draw any meaningful conclusions.

Visualization with Scatter Plots and Trend Lines

A scatter plot is one of the most effective ways to visualize relationships between two numeric variables. In exploratory data analysis (EDA), scatter plots allow us to see trends, patterns, and potential associations at a glance. For instance, by plotting ad_spend (monthly advertising spend) on the x-axis and revenue (monthly sales revenue) on the y-axis, we can examine how advertising investments might influence sales outcomes—a key relationship for a digital advertising agency as they optimize their marketing strategies.

We studied scatter plot basics and visualizations at length in the chapter on visualization. Here, we add a valuable component to help quantify relationships between variables: a trend line. A trend line provides a visual summary of the overall direction and strength of the relationship between two variables, giving us an idea of the effect size—or how much one variable influences the other.

Adding Trend Lines to Scatter Plots with geom_smooth

In R’s ggplot2, we use geom_smooth() to add trend lines to scatter plots. There are two commonly used methods:

  1. Linear Regression (method = "lm"): This fits a straight line to the data, summarizing the relationship between variables with a simple linear trend.
    • When to Use: Linear regression is best when you believe there is a linear relationship between variables (e.g., when one variable increases, the other increases or decreases consistently).
    • Example: We might assume a roughly linear relationship between advertising spend and revenue—higher spend generally leads to higher revenue.
  2. Local Regression (method = "loess"): This fits a smooth, non-linear line that adapts to the shape of the data. It’s more flexible than linear regression, capturing curved or non-linear relationships.
    • When to Use: Use loess when you suspect the relationship might be more complex and not strictly linear. This method is ideal for capturing patterns that don’t fit a straight line.
    • Example: If advertising effects show diminishing returns (e.g., after a certain point, additional spending doesn’t boost revenue as much), loess may better capture this non-linear trend.

To illustrate scatter plots and trend lines, let’s use a new dataset named marketing_data that represents monthly data for AdBoost Solutions, a startup specializing in digital marketing services for small- and medium-sized businesses. This dataset includes several key variables:

  • ad_spend: The amount spent on advertising each month (in dollars).
  • revenue: Monthly sales revenue (in dollars), which is influenced by the advertising spend.
  • region: The geographic region where AdBoost Solutions is running the campaign, categorized as North, South, or East. These regions have different average revenue levels, reflecting variations in customer spending behavior across regions.
  • channel: The advertising channel used for the campaign, with categories of Social Media, Search, and Display Ads. Each channel has a different average impact on revenue, capturing the varying effectiveness of different digital marketing strategies.
  • success: A binary variable indicating whether the campaign was successful, with “Yes” or “No” values. Campaigns with higher advertising spend and revenue have a higher likelihood of success, and certain channels, such as Social Media, are generally more successful for AdBoost Solutions.

This dataset allows us to explore the relationship between advertising spend and revenue—a critical analysis for businesses looking to optimize their marketing budgets and maximize returns. Here is a glimpse of the dataset.

Rows: 100
Columns: 5
$ ad_spend <dbl> 1080, 3516, 1984, 1417, 2157, 4020, 1393, 1486, 2489, 3390, 8…
$ revenue  <dbl> 18613, 19315, 19495, 19706, 16657, 17982, 20716, 18764, 18326…
$ region   <chr> "South", "East", "South", "South", "East", "East", "North", "…
$ channel  <chr> "Social Media", "Search", "Search", "Search", "Display Ads", …
$ success  <chr> "Yes", "Yes", "Yes", "Yes", "No", "No", "Yes", "No", "Yes", "…

First, let’s explore the relationship between ad_spend and revenue as a linear relationship in a scatter plot.

# Load ggplot2
library(ggplot2)

# Scatter plot with linear regression (lm) trend line
ggplot(marketing_data, aes(x = ad_spend, y = revenue)) +
  geom_point() +
  geom_smooth(method = "lm", se = FALSE, color = "dodgerblue3", linewidth = 2) +
  labs(title = "Ad Spend vs. Revenue with Linear Trend Line",
       x = "Advertising Spend",
       y = "Monthly Revenue")  +  
  scale_x_continuous(labels = dollar) +  # Format y-axis as currency  
  scale_y_continuous(labels = dollar) +  # Format y-axis as currency
  theme_minimal()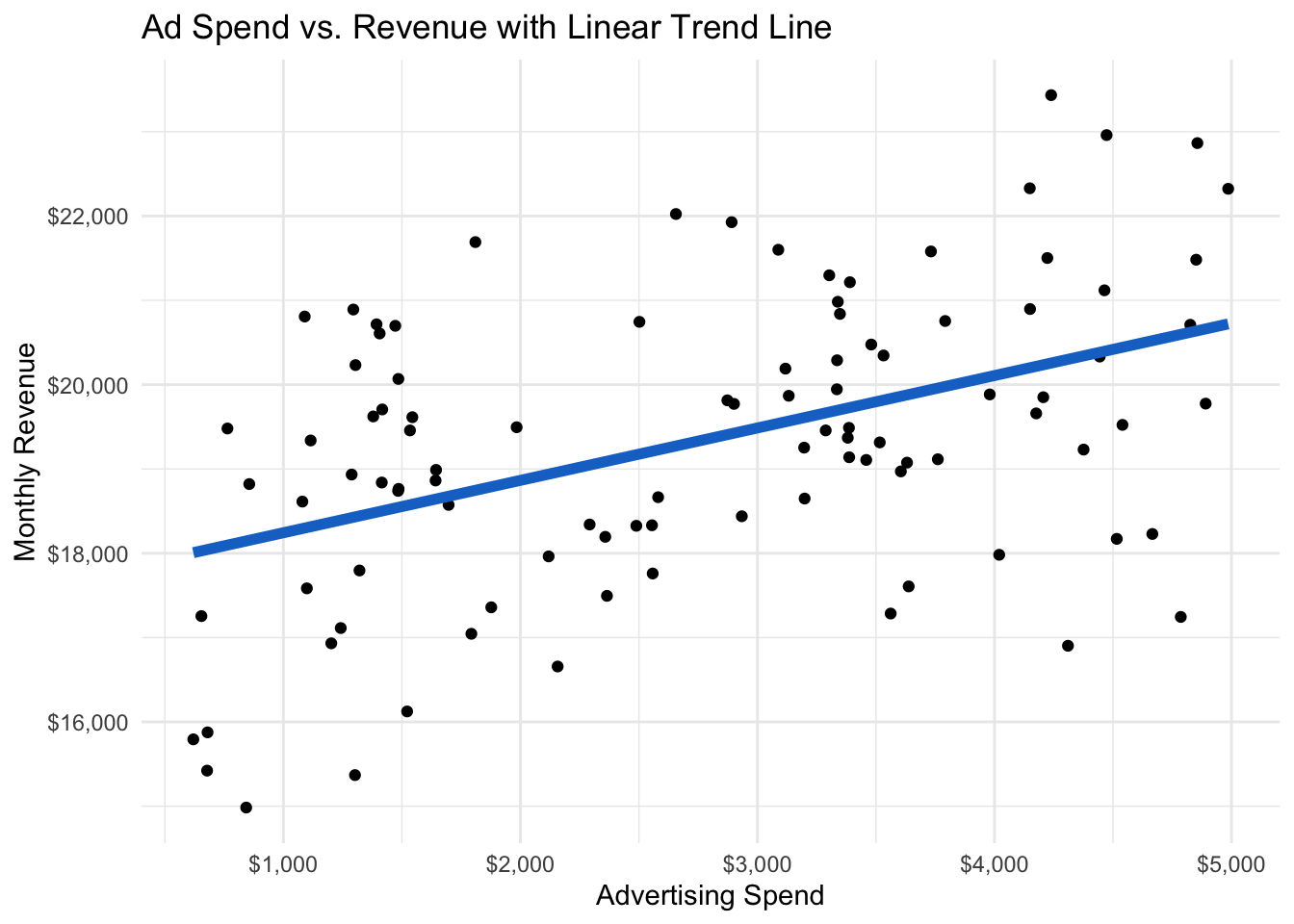
Figure 24.3: A scatterplot of the relationship between spending on advertising and monthly revenue among AdBoost Solutions’ clients with a linear trend lines,

In Figure 24.3, the linear trend line is consistently above the actual data for low levels of advertising. This suggests that the relationship may not be linear. We can check by generating the scatter plot with a non-linear trend line.

Figure 24.4: A scatterplot of the relationship between spending on advertising and monthly revenue among AdBoost Solutions’ clients with a non-linear trend line.

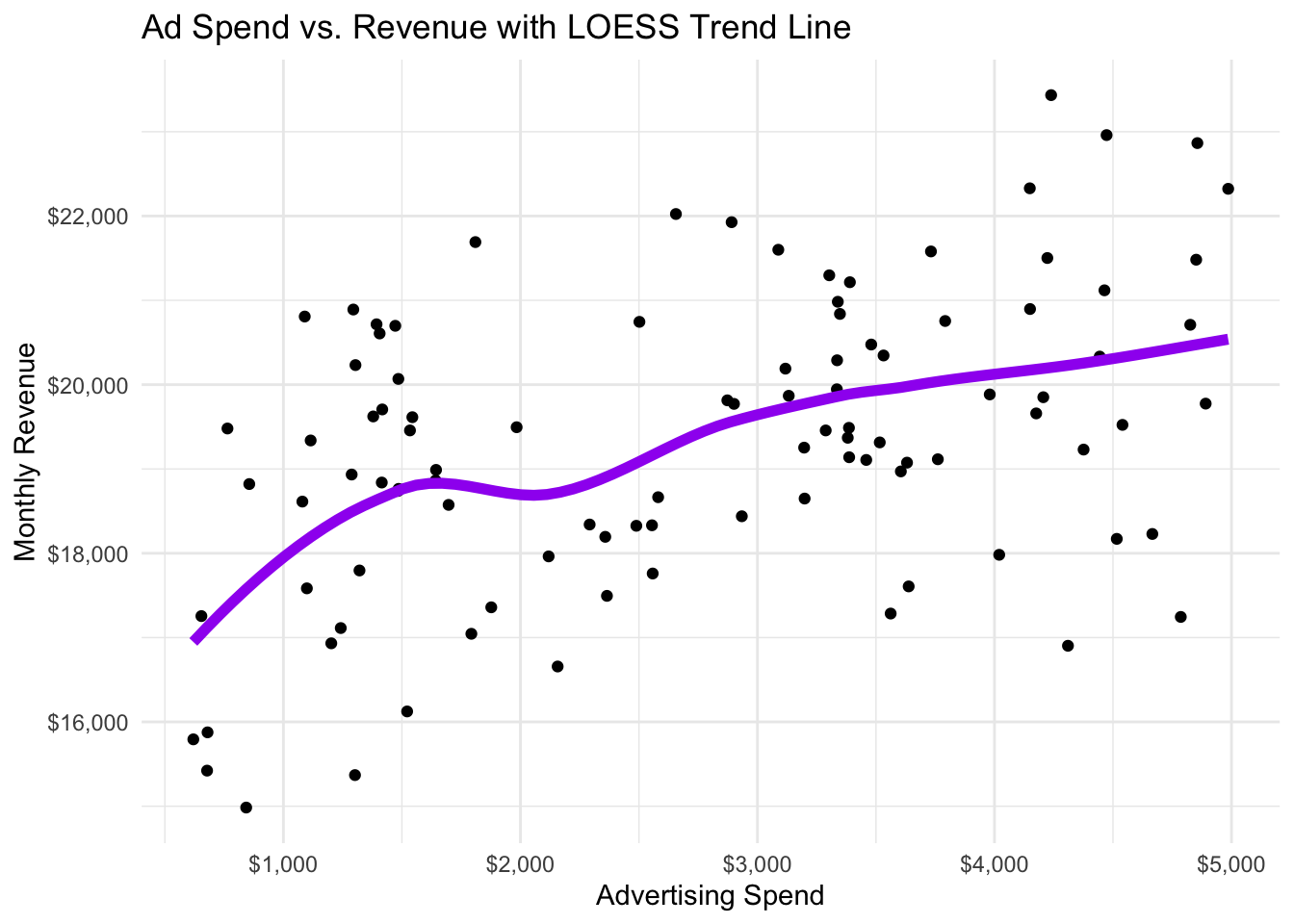
Interpretation: It is clear that there is positive correlation between advertising spending ad_spend and revenue. Based on the scatter plot and the closer fit of the non-linear trend line in Figure 24.4, we find evidence for a non-linear relationship where revenue goes up with ad spending but at a decreasing rate. This evidence is further supported by the results of correlation calculations:

  • Pearson Correlation: 0.45
  • Spearman Correlation: 0.4

Scatter plots with trend lines are powerful tools for visualizing relationships between numeric variables. By choosing an appropriate trend line method (lm or loess), we can highlight the nature of the relationship. Adding a correlation coefficient allows us to quantify the strength of this relationship, helping entrepreneurs make data-driven decisions based on the observed trends.

Demonstration: Visualization of Correlation with Scatter Plots

In ggplot2, we can further enhance scatter plots by adding trend lines to visualize the direction of the relationship.

# Load ggplot2 for visualization
library(ggplot2)

# Basic scatter plot with trend line
linear_trend_plot <- ggplot(customer_data, aes(x = age, y = spending)) +
  geom_point() +
  geom_smooth(method = "lm", se = FALSE, color = "steelblue", linewidth = 2) +
  labs(title = "Age vs. Spending with Linear Trend Line",
       x = "Age",
       y = "Spending") +
  theme_minimal() +
  theme(plot.title = element_text(size = 18))

loess_trend_plot <- ggplot(customer_data, aes(x = age, y = spending)) +
  geom_point() +
  geom_smooth(method = "loess", se = FALSE, color = "purple", linewidth = 2) +
  labs(title = "Age vs. Spending with Non-linear Trend Line",
       x = "Age",
       y = "Spending") +
  theme_minimal() +
  theme(plot.title = element_text(size = 18))

# Arrange Pearson and Spearman plots side by side using cowplot
library(cowplot)

#plot_grid(pearson_plot, spearman_plot, labels = c("A", "B"), ncol = 2)
plot_grid(linear_trend_plot, loess_trend_plot, ncol = 2)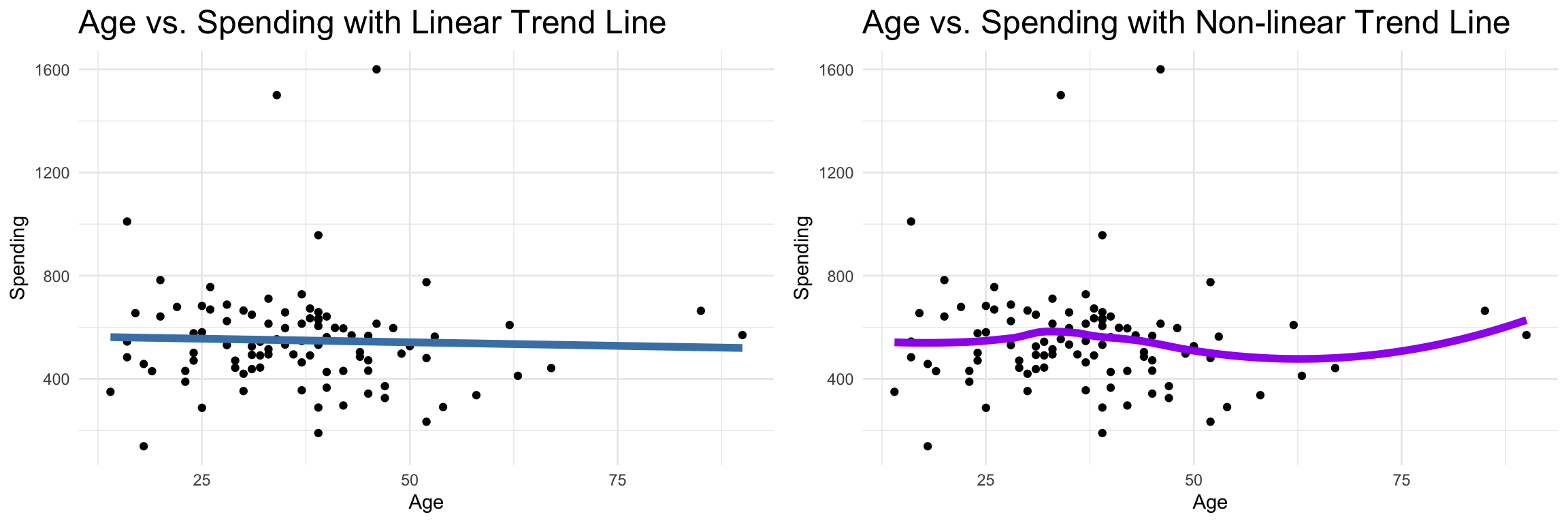
Figure 24.5: A scatterplot of the relationship between age and spending among UrbanFind’s customers, with linear and non-linear trend lines.

Insight: The flat, negative correlation between age and spending supports the low correlation statistics found above indicating a weak relationship between the two variables.

It is possible that the relationship between age and spending is stronger for some products than for others. Let’s add additional layers of insight by plotting with color points and trend lines by a third variable (product_interest).

# Scatter plot with third variable (product_interest) color-coded
ggplot(customer_data, aes(x = age, y = spending, color = product_interest)) +
  geom_point() +
  geom_smooth(method = "lm", se = FALSE, linewidth = 1.5) +
  labs(title = "Scatter Plot of Age vs. Spending by Product Interest",
       x = "Age",
       y = "Spending",
       color = "Product Interest") +
  theme_minimal()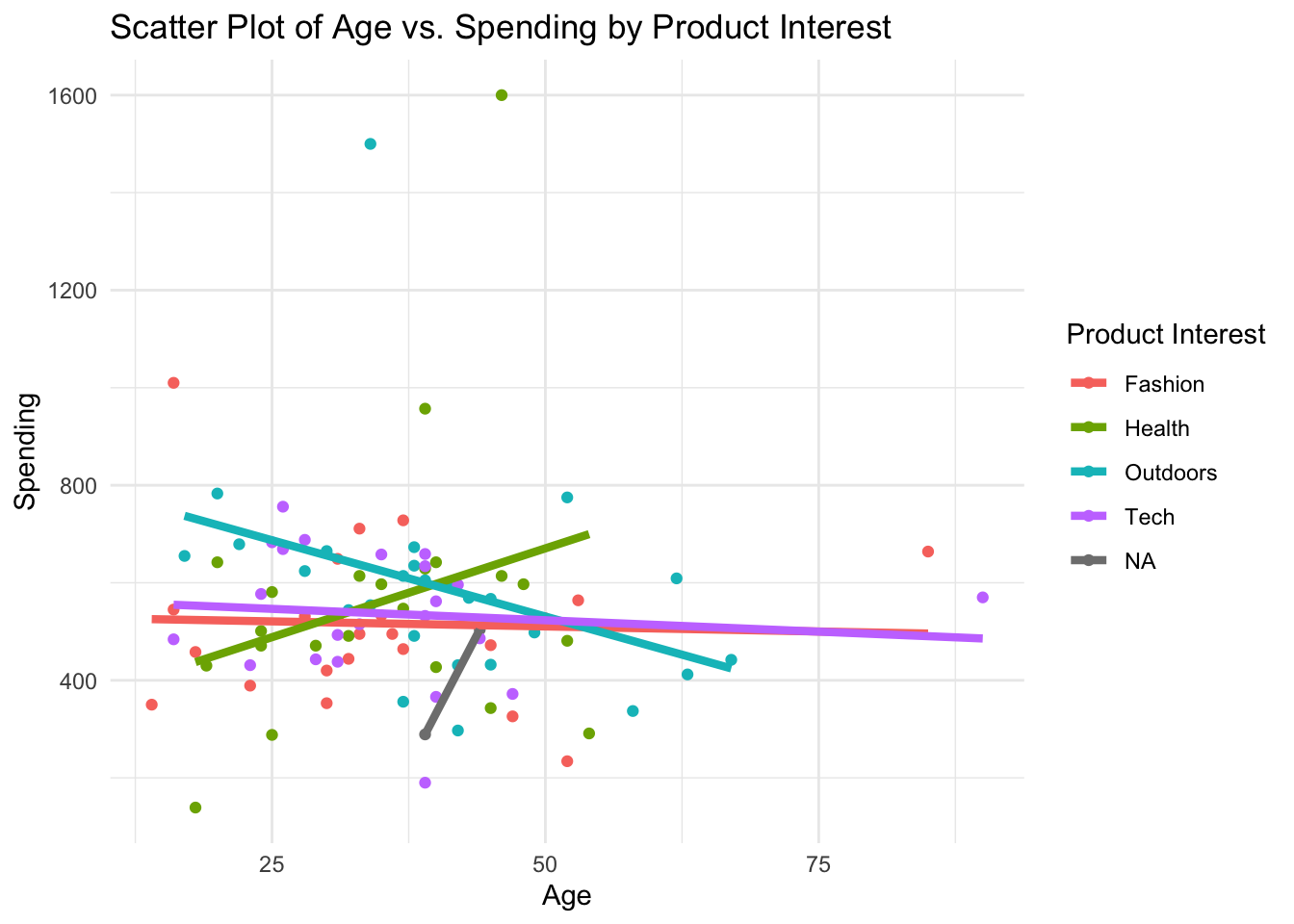
Figure 24.6: A scatterplot of age vs spending with trend lines for all products of interest.

Insight: Separating the effects of the relationship between age and spending among UrbanFind’s customers gives much deeper insight into the releationship. The overall relationship between age and spending is negative but weak. The weak relationship is actually the result of combining some near-zero relationships with some strong positive and strong negative relationships for different products.”

Exercise: Numeric-Numeric EDA Analysis

Try it yourself:

To explore numeric-numeric relationships, we’ll be using the sales_data dataset from MetroMart, first introduced in Chapter 23.4.4. MetroMart is a fictional retail company operating across multiple regions, selling a variety of products across different categories.

Here’s a quick reminder of the data and variables:

  • Product ID: A unique identifier for each product.
  • Price: The selling price of each product.
  • Quantity Sold: The number of units sold.
  • Region: The region (North, South, East, or West) where the sale took place.
  • Category: The product category (Electronics, Grocery, Clothing, or Home Goods).
  • Promotion: Indicates if the product was on promotion (Yes or No).

Using the MetroMart dataset, answer the following questions about the relationship between price and quantity_sold:

  1. What is the correlation between price and quantity_sold? How much do the Pearson and Spearman measures of correlation differ?
  2. Generate a scatterplot of the relationship between price and quantity_sold. Experiment with adding the trend line and changing the method (e.g., lm for linear and loess for non-linear relationships) to see how it affects your interpretation.
  3. Does coloring the scatterplot and trend lines by category or promotion reveal any interesting patterns?

Hint 1

  1. Calculate the covariance for the relationship between price and quantity_sold. Then calculate the Pearson and Spearman correlation coefficients for the relationship.

  2. Generate a scatterplot of the relationship between price and quantity_sold. Add a linear trend line then try a non-linear (loess) trend line

  3. Color the scatterplot by category and promotion to identify how the relationship changes by these variables.

Hint 2

  1. Covariance and correlation

    1. Call the cov() function specifying sales_data$price and sales_data$quantity_sold as the variables.
    2. Call the cor() function for the same variables using the Pearson method
    3. Call the cor() function for the same variables using the Spearman method

  2. Visualize the relationship

    1. Call the ggplot() function
    2. Specify the data as sales_data
    3. Map the aesthetic with x = price and y = quantity_sold
    4. Specify the geometry as `geom_point()
    5. Add the trend line using the geometry geom_smooth() with the appropriate methods

  3. Visualize the conditional relationship

    1. Generate the scatterplot as described above
    2. In the ggplot aesthetic, set color to category
    3. In another plot, set the color of the ggplot aesthetic to promotion

Fully worked solution:

1cov(sales_data$price, sales_data$quantity_sold, use = "complete.obs")
2cor(sales_data$price, sales_data$quantity_sold,  use = "complete.obs", method = "pearson")
cor(sales_data$price, sales_data$quantity_sold,  use = "complete.obs", method = "spearman")

3ggplot(sales_data,
  aes(x = price, y = quantity_sold)) +
  geom_point() +
4  geom_smooth(method = "lm", se = FALSE, color = "red") +
  theme_minimal()

ggplot(sales_data,                      
5  aes(x = price, y = quantity_sold, color = category)) +
  geom_point() +                        
  geom_smooth(method = "lm", se = FALSE, linewidth = 1.5) +
  theme_minimal()
1
Call the cov() function to calculate the covariance
2
Call the cor() function to calculate the correlation coefficient using the Pearson and Spearman methods
3
Call the ggplot() function and specify sales_data and specify that aesthetic mapping with x = price and y = quantity_sold. Specify geom_point() for scatterplot
4
Add the geom_smooth(method = "lm) to get a linear trend line
5
Add color = category or color = promotion to the ggplot aesthetic
  1. What differences do you observe between the linear (lm) and non-linear (loess) trend lines? Which trend line better captures the relationship between price and quantity_sold?
  2. Given the diminishing quantity sold at higher prices, which trend line would you consider more appropriate for understanding customer response to price increases?
  3. Does the relationship between price and quantity_sold appear to differ by product category? Are some product categories more or less sensitive to price changes?
  4. Using the linear (lm) and non-linear (loess) trend lines, do you notice any patterns within specific product categories that stand out in the relationship between price and quantity_sold?
  5. How does the trend in quantity_sold differ when products are on promotion versus when they are not? Does the linear or non-linear trend line reveal any notable differences in sales patterns between promoted and non-promoted items?
  6. Based on the plots with color = promotion, which trend line approach (linear or non-linear) helps you better understand the influence of promotions on the price-quantity relationship?
  7. How does the choice of trend line and color grouping affect your interpretation of the data?
  8. Imagine you are advising MetroMart on their pricing strategy. What insights about the price-quantity relationship and the role of promotions could help them make data-driven decisions?


24.3 Numeric-Categorical Analysis

When examining relationships between a categorical and a numeric variable, we can use both statistical tests and visualizations to assess how the numeric variable behaves across categories. This type of analysis can help us understand differences in central tendency, spread, and overall distribution within each category.

To understand numeric data distributions across categories, we often start by comparing means and medians within each category. Statistical tests, such as t-tests or ANOVA (Analysis of Variance), help us determine whether one category tends to have higher or lower values than another and whether those observed differences between categories are statistically significant.

T-Tests: Comparing Means between Two Groups

A t-test is a statistical test used to determine whether the means of a numeric variable differ significantly between two groups. This test is particularly useful in business analytics when we want to understand if two groups (such as different regions or marketing channels) have different average outcomes.

Why Use a T-Test?

In data analysis, we often need to determine if observed differences between groups are likely to be real or just due to random chance. The t-test provides a formal way to test this, helping us decide if the difference in means between two groups is statistically significant.

  • Null Hypothesis: The t-test assumes there is no difference between the group means.
  • Alternative Hypothesis: The t-test tests against the possibility that there is a difference between the group means.

If the t-test shows a statistically significant result, we have evidence to reject the null hypothesis and conclude that the two groups differ meaningfully in their means.

The T-Distribution

The t-distribution is the theoretical distribution used to calculate the test statistic in a t-test. It resembles a normal distribution but has heavier tails, which accounts for variability in small samples.

To help visualize this, here is a plot of the t-distribution alongside the normal distribution:

Figure 24.7: A plot of a normal distribution and a t-distribution illustrating the thicker tails of the t-distribution.

In this plot, the t-distribution (solid blue line) has heavier tails, meaning it’s more spread out at the ends than the normal distribution (dashed red line). This accounts for increased variability, especially in small sample sizes.

Conducting a T-Test

The t-test calculates a t-statistic, which measures how far apart the group means are, relative to the variability within each group. The t-statistic formula is:

\[ \mathsf{t = \dfrac{\textsf{difference in group means}}{\textsf{standard error of the difference}}} \]

The t-statistic is then compared to a critical value in the t-distribution to determine whether the difference in means is statistically significant.

Example in AdBoost Solutions: Testing Revenue Differences by Region

Suppose we want to test whether average revenue differs significantly between the North and South regions.

  1. Set Up the Hypotheses:

    • Null Hypothesis (H₀): The mean revenue is the same in both regions.
    • Alternative Hypothesis (H₁): The mean revenue differs between the regions.

  2. Run the T-Test:

# Perform a t-test comparing revenue between North and South regions in AdBoost data
t_test_result <- t.test(revenue ~ region, 
                        data = marketing_data |> 
                          filter(region %in% c("North", "South")))
t_test_result

  1. Interpret the Result:

    • The p-value in the output tells us the probability of observing a difference as large as (or larger than) the one found, assuming the null hypothesis is true.
    • If the p-value is less than our significance level (commonly 0.05), we reject the null hypothesis and conclude that there is a statistically significant difference in mean revenue between the North and South regions.
Key Points for Interpretation
  • T-Statistic: The larger the t-statistic, the greater the evidence against the null hypothesis.
  • P-Value: A low p-value (typically < 0.05) indicates that the observed difference is unlikely to have occurred by random chance.

Choosing the Right T-Test

There are two main types of t-tests for comparing two groups:

  • Independent T-Test (also known as a two-sample t-test): Used when the groups are independent of each other, such as North vs. South regions.
  • Paired T-Test: Used when observations in one group are paired with observations in the other (e.g., measurements before and after a treatment on the same subjects).

In most business contexts, we use the independent t-test for comparing metrics like revenue across different groups.

Applying the T-Test: Revenue Differences by Region

Objective of the T-Test

The purpose of a t-test is to help us understand if any observed difference in means between two groups is likely due to chance or if it’s statistically significant. In our context, we want to know if there’s a meaningful difference in average revenue between two regions.

  • Null Hypothesis (H₀): The average revenue is the same in both the North and South regions.
  • Alternative Hypothesis (H₁): The average revenue differs between these two regions.
Running the T-Test

In AdBoost Solutions’ marketing_data, we can test for revenue differences between the North and South regions with the following code:

# Perform a t-test comparing revenue between North and South regions
t_test_result <- t.test(revenue ~ region, 
                        data = marketing_data |> 
                          filter(region %in% c("North", "South")))
t_test_result

    Welch Two Sample t-test

data:  revenue by region
t = 2.1608, df = 63.298, p-value = 0.0345
alternative hypothesis: true difference in means between group North and group South is not equal to 0
95 percent confidence interval:
   62.30117 1592.94883
sample estimates:
mean in group North mean in group South 
           20386.25            19558.62

Interpretation: The results of our t-test to determine if average revenue differs between the North and South regions yield a t-statistic of t = 2.1608, with a p-value of p = 0.0345. Given this p-value, which is below the commonly used significance threshold of 0.05, we reject the null hypothesis that revenue is the same in the North and South regions. We conclude that there is a statistically significant difference in average revenue between the North and South regions.

Visualizing the T-Test Result

To support the t-test findings, we can use a box plot to show the revenue distribution in each region. This visualization gives us a clearer picture of how revenue values vary within each region.

# Box plot for revenue by region
ggplot(marketing_data |> filter(region %in% c("North", "South")), aes(x = region, y = revenue)) +
  geom_boxplot() +
  labs(title = "Revenue by Region", x = "Region", y = "Revenue") +
  scale_y_continuous(labels = dollar) +  # Format y-axis as currency  
  theme_minimal()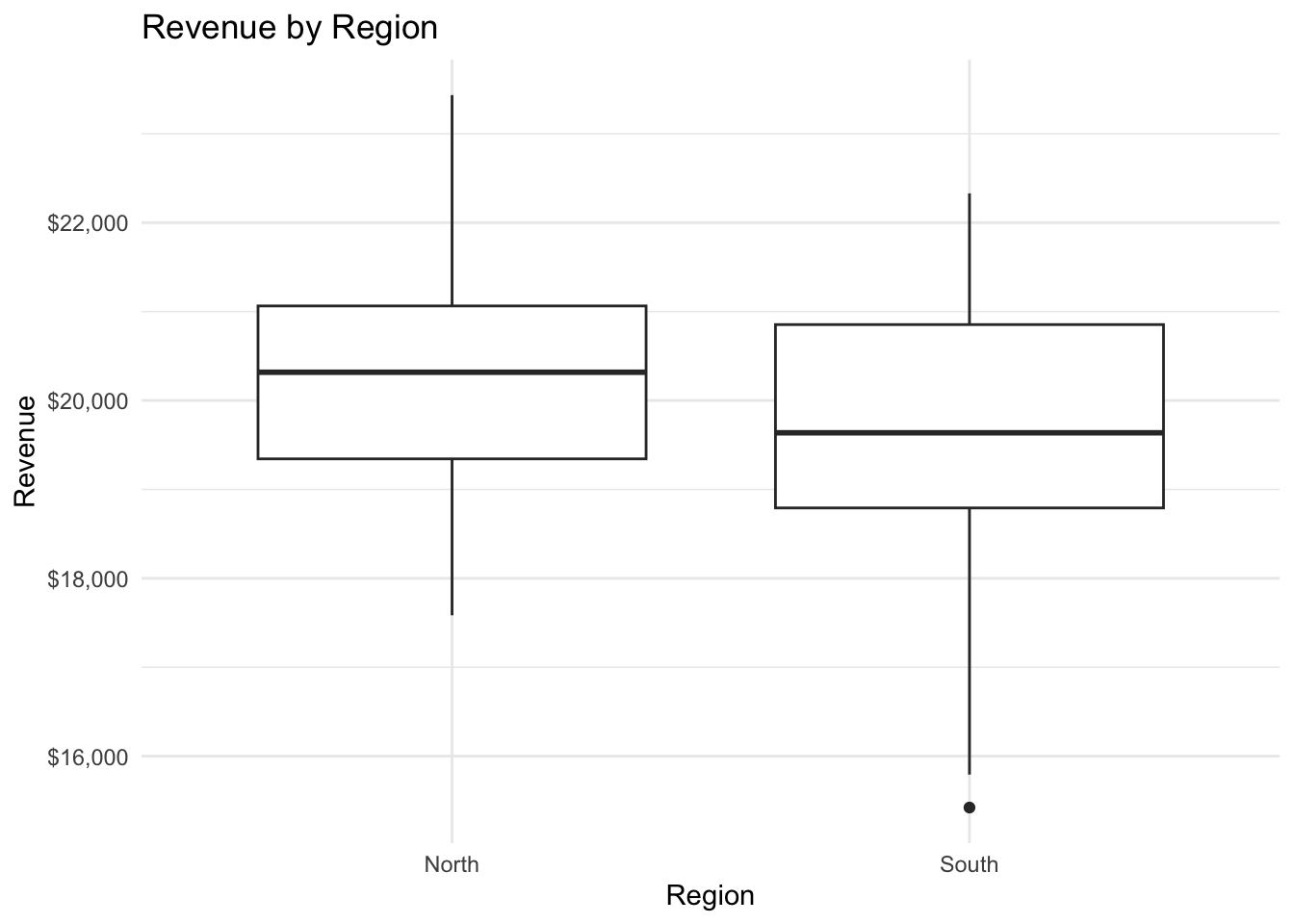

This plot helps us see differences in the median, spread, and any potential outliers for revenue between the North and South regions, reinforcing the t-test results.

ANOVA: Analyzing Differences Across Multiple Groups

When comparing more than two groups, an ANOVA (Analysis of Variance) test helps determine if there are statistically significant differences in means across these groups. For example, AdBoost Solutions might want to test if average revenue differs across the three advertising channels: Social Media, Search, and Display Ads.

Purpose of ANOVA

The goal of ANOVA is to test whether at least one group mean is different from the others. It uses the F-test to compare the variance within groups to the variance between groups. If the variance between groups is significantly larger than the variance within groups, we have evidence that at least one group’s mean is different.

  • Null Hypothesis (H₀): All group means are equal.
  • Alternative Hypothesis (H₁): At least one group mean differs from the others.

The F-Test in ANOVA

The F-test produces an F-statistic, which measures the ratio of variance between groups to the variance within groups:

  • A larger F-statistic suggests a greater likelihood that the group means differ.
  • The p-value associated with the F-statistic tells us if this difference is statistically significant.

If the p-value is below a chosen significance level (commonly 0.05), we reject the null hypothesis and conclude that at least one group mean is different from the others.

The relevant question is not whether ANOVA assumptions are met exactly, but rather whether the plausible violations of the assumptions have serious consequences on the validity of probability statements based on the standard assumptions.
— – Gene V. Glass & Percy D. Peckham & James R. Sanders, Consequences of Failure to Meet Assumptions Underlying the Fixed Effects Analyses of Variance and Covariance, Review of Educational Research Vol. 42, No. 3 (Summer, 1972), pp. 237-288 , p. 237.

– Gene V. Glass & Percy D. Peckham & James R. Sanders, Consequences of Failure to Meet Assumptions Underlying the Fixed Effects Analyses of Variance and Covariance, Review of Educational Research Vol. 42, No. 3 (Summer, 1972), pp. 237-288 , p. 237. (#statistics,anova)

Example in AdBoost Solutions: Revenue Differences Across Channels

Let’s perform an ANOVA test to assess whether mean revenue differs across the three advertising channels (Social Media, Search, Display Ads) in AdBoost’s marketing_data.

Running the ANOVA Test
# Perform ANOVA to test for revenue differences across advertising channels
anova_result <- aov(revenue ~ channel, data = marketing_data)
summary(anova_result)
            Df   Sum Sq  Mean Sq F value   Pr(>F)    
channel      2 9.72e+07 48601175      23 6.69e-09 ***
Residuals   97 2.05e+08  2113273                     
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Interpreting ANOVA Output
  • F-Statistic: A higher F-statistic indicates a greater likelihood that there’s a difference in revenue between the channels.
  • P-Value: A p-value below 0.05 suggests that the observed differences in revenue across channels are unlikely due to random chance. We would then conclude that there is a statistically significant difference in average revenue among the advertising channels.

Interpretation: The output of this test includes the F-statistic of F = 22.9981 and p-value of p = 0.000000006687. Based on the p-value, we may reject the null hypothesis and conclude that at least one group mean differs from the others.

Visualizing Revenue Differences by Channel

We can use a box plot to visually compare revenue distributions across channels. This visualization reinforces the ANOVA results, showing the spread and central tendency of revenue in each channel.

# Box plot for revenue by channel
ggplot(marketing_data, aes(x = channel, y = revenue)) +
  geom_boxplot() +
  labs(title = "Revenue by Advertising Channel", x = "Channel", y = "Revenue") +
  theme_minimal()

The box plot allows us to see if any channels have consistently higher or lower revenues and provides a visual summary of revenue variability within each channel.

Tukey’s HSD Test

If ANOVA shows a significant difference, we can conduct post hoc tests to identify which channels differ. Tukey’s HSD (Honest Significant Difference) test is a common choice.

# Perform Tukey's HSD post hoc test for pairwise comparisons
tukey_result <- TukeyHSD(anova_result)
tukey_result
  Tukey multiple comparisons of means
    95% family-wise confidence level

Fit: aov(formula = revenue ~ channel, data = marketing_data)

$channel
                             diff       lwr      upr     p adj
Search-Display Ads       1230.543  377.3606 2083.725 0.0025118
Social Media-Display Ads 2340.898 1517.5649 3164.231 0.0000000
Social Media-Search      1110.355  229.6411 1991.069 0.0095050

Interpreting Tukey’s HSD Test Results

The Tukey HSD (Honestly Significant Difference) test compares the means between pairs of categories and tells us if these differences are statistically significant. Here’s how to interpret each part of the output:

  • Comparison (e.g., Search-Display Ads): Each row compares the average revenue between two advertising channels. For example, Search-Display Ads shows the difference in mean revenue between Search and Display Ads.

  • diff: This is the difference in average revenue between the two channels. A positive value means that the first group in the comparison (e.g., Search) has a higher average revenue than the second group (e.g., Display Ads). A negative value would mean the opposite.

  • lwr and upr: These are the lower and upper bounds of the 95% confidence interval for the mean difference. If this interval doesn’t contain zero, we have evidence that the difference is statistically significant.

  • p adj: This is the adjusted p-value, which accounts for the fact that we are making multiple comparisons. A p-value below 0.05 suggests a statistically significant difference between the two groups.

Results for AdBoost Channels

From the output of Tukey’s HSD test, we find:

  • Search-Display Ads: The average revenue for Search is 1230.5426 units higher than for Display Ads. With a p-value of 0.0025, this difference is statistically significant.
  • Social Media-Display Ads: The average revenue for Social Media is 2340.8979 units higher than for Display Ads. This is also statistically significant, with a p-value that is effectively NA (<0.0001).
  • Social Media-Search: The average revenue for Social Media is 1110.3553 units higher than for Search, with a significant p-value of 0.0095

The Tukey test shows that:

  • Social Media generates significantly higher revenue than both Display Ads and Search.
  • Search generates significantly higher revenue than Display Ads.

These insights indicate that Social Media is the highest-performing channel in terms of revenue, followed by Search, with Display Ads generating the lowest average revenue. This information can help in deciding which channels to prioritize.

Exercise: Numeric-Categorical EDA Analysis

Try it yourself:

In this exercise, we return to the sales_data dataset from MetroMart, first introduced in Chapter 23.4.4. MetroMart is a fictional retail company operating across multiple regions, selling a variety of products in different categories.

Here’s a quick reminder of some key variables we’ll use in this exercise:

  • Price: The selling price of each product.
  • Quantity Sold: The number of units sold.
  • Category: The product category (Electronics, Grocery, Clothing, or Home Goods).
  • Promotion: Indicates whether the product was on promotion (Yes or No).

In this section, we’ll focus on understanding how price and quantity sold vary across different categories and promotion statuses.

  1. Comparing Price by Product Category

    • Use an ANOVA test to determine if there are statistically significant differences in price across the four product categories (category).
    • Visualize the distribution of price by category using a box plot.

  2. Analyzing the Impact of Promotions on Quantity Sold

    • Conduct a t-test to compare the average quantity_sold between products that were on promotion (Promotion = Yes) and those that were not (Promotion = No).
    • Create a box plot of quantity_sold grouped by promotion.

  3. Exploring Sales Patterns Across Categories: Generate box plots of quantity_sold across each category to see how sales volume varies among different types of products.

  4. Combining Category and Promotion to Examine Price Sensitivity: Create box plots of quantity_sold by promotion, but split the data further by category (e.g., side-by-side plots for each category).

Hint 1

  1. Perform the ANOVA test of price across categories. Then, if the ANOVA test shows significant differences, perform the TukeyHSD test. Then generate a box plot of price across categories

  2. Perform the t-test of quantity sold across promotion status. Then generate a box plot of quantity sold across promotion status

  3. Generate a box plot of quantity sold across categories

  4. Generate a box plot of price across promotion status split across categories (hint in a hint: consider facet_grid() for creating another layer of splitting)

Hint 2

  1. ANOVA of price across categories

    1. Call the aov() function specifying the numeric variable (price) as the y variable and the categorical variable (category) as the x variable
    2. If the ANOVA test is significant, call the TukeyHSD() function specifying the ANOVA results as the input
    3. Call the ggplot() function, specify the data as sales_data, map the aesthetic with x = category and y = price specify the geometry as `geom_boxplot()

  2. Analyzing the Impact of Promotions on Quantity Sold

    1. Call the t.test() function specifying data as sales_data, quantity_sold (numeric variable) as the y-variable and promotion (categorical variable) as the x variable
    2. Call the ggplot() function, specify the data as sales_data, map the aesthetic with x = promotion and y = quantity_sold, specify the geometry as `geom_boxplot()

  3. Exploring Sales Patterns Across Categories

    1. Call the ggplot() function, specify the data as sales_data, map the aesthetic with x = category and y = quantity_sold, specify the geometry as `geom_boxplot()

  4. Combining Category and Promotion to Examine Price Sensitivity

    1. Call the ggplot() function, specify the data as sales_data, map the aesthetic with x = promotion and y = price, specify the geometry as `geom_boxplot(), specify facet_grid as category; OR
    2. Create a new promo_category variable that combines promotion and category, call the ggplot() function, specify the data as sales_data, map the aesthetic with x = promo_category and y = price, specify the geometry as `geom_boxplot()

Fully worked solution:

# 1.1 Perform ANOVA to test for price differences across categories
anova_result <- aov(price ~ category, data = sales_data)
summary(anova_result)
# 1.2 If ANOVA results are significant, perform a Tukey HSD test to identify which categories differ
# ANOVA results are not significant - performing Tukey HSD test anyway
# Perform Tukey's HSD post hoc test for pairwise comparisons
tukey_result <- TukeyHSD(anova_result)
tukey_result
# 1.2 Visualize the distribution of price by category using a box plot.
ggplot(sales_data, aes(x = category, y = price)) +
  geom_boxplot() +
  labs(title = "Price by Category", x = "Category", y = "Price") +
  theme_minimal()

# 2.1 Conduct a t-test to compare the average quantity_sold between products that were on promotion (Promotion = Yes) and those that were not (Promotion = No).
t_test_result <- t.test(quantity_sold ~ promotion, 
                        data = sales_data |> 
                          filter(promotion %in% c("Yes", "No")))
t_test_result
# 2.2 Create a box plot of quantity_sold grouped by promotion.
ggplot(sales_data |> filter(promotion %in% c("Yes", "No")), aes(x = promotion, y = quantity_sold)) +
  geom_boxplot() +
  labs(title = "Quantity Sold by Promotion Status", x = "Promotion", y = "Quantity Sold") +
  theme_minimal()
  
# 3. Generate box plots of quantity_sold across each category to see how sales volume varies among different types of products.
ggplot(sales_data, aes(x = category, y = quantity_sold)) +
  geom_boxplot() +
  labs(title = "Quantity Sold by Category", x = "Category", y = "Quantity Sold") +
  theme_minimal()

#4. Create box plots of quantity_sold by promotion, but split the data further by category (e.g., side-by-side plots for each category).
# Using facets to create another dimension on category
ggplot(sales_data, aes(x = promotion, y = quantity_sold)) +
  geom_boxplot() +
  facet_grid(~ category) +
  labs(
    title = "Quantity Sold by Promotion Status, Split by Category",
    x = "Promotion Status",
    y = "Quantity Sold"
  ) +
  theme_minimal()
#### OR
# Create a new variable that combines promotion and category
sales_data$promo_category <- interaction(sales_data$promotion, sales_data$category, sep = " - ")
# Plot using the combined promo_category variable
ggplot(sales_data, aes(x = promo_category, y = quantity_sold)) +
  geom_boxplot() +
  labs(
    title = "Quantity Sold by Promotion Status and Category",
    x = "Promotion - Category",
    y = "Quantity Sold"
  ) +
  theme_minimal() +
  theme(axis.text.x = element_text(angle = 45, hjust = 1))  # Tilt x-axis labels for readability

  1. Comparing Price by Product Category: Based on the ANOVA and the visualization, which categories have the highest and lowest average prices? Are there any notable differences in the spread of prices within each category?

  2. Analyzing the Impact of Promotions on Quantity Sold: Based on the t-test results and the plot, what can you conclude about the effect of promotions on quantity sold? Do promotions seem to increase sales?

  3. Exploring Sales Patterns Across Categories: Describe any differences you observe in the distribution of quantity_sold for each category. Are there particular categories that seem to have higher sales volumes or greater variability in sales?

  4. Combining Category and Promotion to Examine Price Sensitivity: What patterns do you notice? For example, do promotions affect some product categories more than others in terms of quantity sold? What might this indicate about price sensitivity across different types of products?


24.4 Categorical-Categorical Analysis

When analyzing two categorical variables, we often want to understand if there’s an association between them. For instance, AdBoost Solutions might want to know if the type of advertising channel is associated with whether a campaign was successful.

Contingency Tables

A contingency table is a useful way to summarize the frequency of observations across categories. It shows how often each combination of categories occurs in the data. By examining these counts, we can see if there appears to be an association between two categorical variables.

For example, let’s create a contingency table for AdBoost’s advertising channels and campaign success statuses.

# Generate a contingency table for 'channel' and 'success'
table(marketing_data$channel, marketing_data$success)
              
               No Yes
  Display Ads  35   3
  Search        5  24
  Social Media  1  32

This table displays the counts for each combination of channel (e.g., Social Media, Search, Display Ads) and success (e.g., Yes, No).

Chi-Square Test for Independence

The chi-square test for independence allows us to test if there’s a statistically significant association between two categorical variables. The test compares the observed frequencies in each category to the frequencies we would expect if the variables were independent.

  • Null Hypothesis (H₀): There is no association between the two categorical variables (they are independent).
  • Alternative Hypothesis (H₁): There is an association between the two categorical variables.

Let’s perform a chi-square test to check if there’s an association between channel and success in AdBoost’s data.

# Perform chi-square test for independence between 'channel' and 'success'
chisq_test <- chisq.test(table(marketing_data$channel, marketing_data$success))
chisq_test

    Pearson's Chi-squared test

data:  table(marketing_data$channel, marketing_data$success)
X-squared = 67.463, df = 2, p-value = 2.242e-15

If the p-value from the test is below a significance level (e.g., 0.05), we reject the null hypothesis and conclude that there is an association between the two variables.

Interpretation: The Chi-squared test returns a p-value of effectively zero (0.000000000000002242). This significant result (p < 0.05) suggests that the choice of channel might impact the likelihood of campaign success, indicating an association between channel and success.

Visualizations

To visualize the relationship between two categorical variables, stacked bar charts and mosaic plots are commonly used.

Stacked Bar Charts

A stacked bar chart shows the distribution of one categorical variable within the levels of another categorical variable. This can help reveal potential associations.

For AdBoost, we’ll create a stacked bar chart of success counts within each channel to see if success rates vary by channel.

# Stacked bar chart of success by channel
library(ggplot2)

ggplot(marketing_data, aes(x = channel, fill = success)) +
  geom_bar(position = "fill") +
  labs(
    title = "Proportion of Campaign Success by Advertising Channel",
    x = "Channel",
    y = "Proportion of Success",
    fill = "Success"
  ) +
  scale_y_continuous(labels = scales::percent) +
  theme_minimal()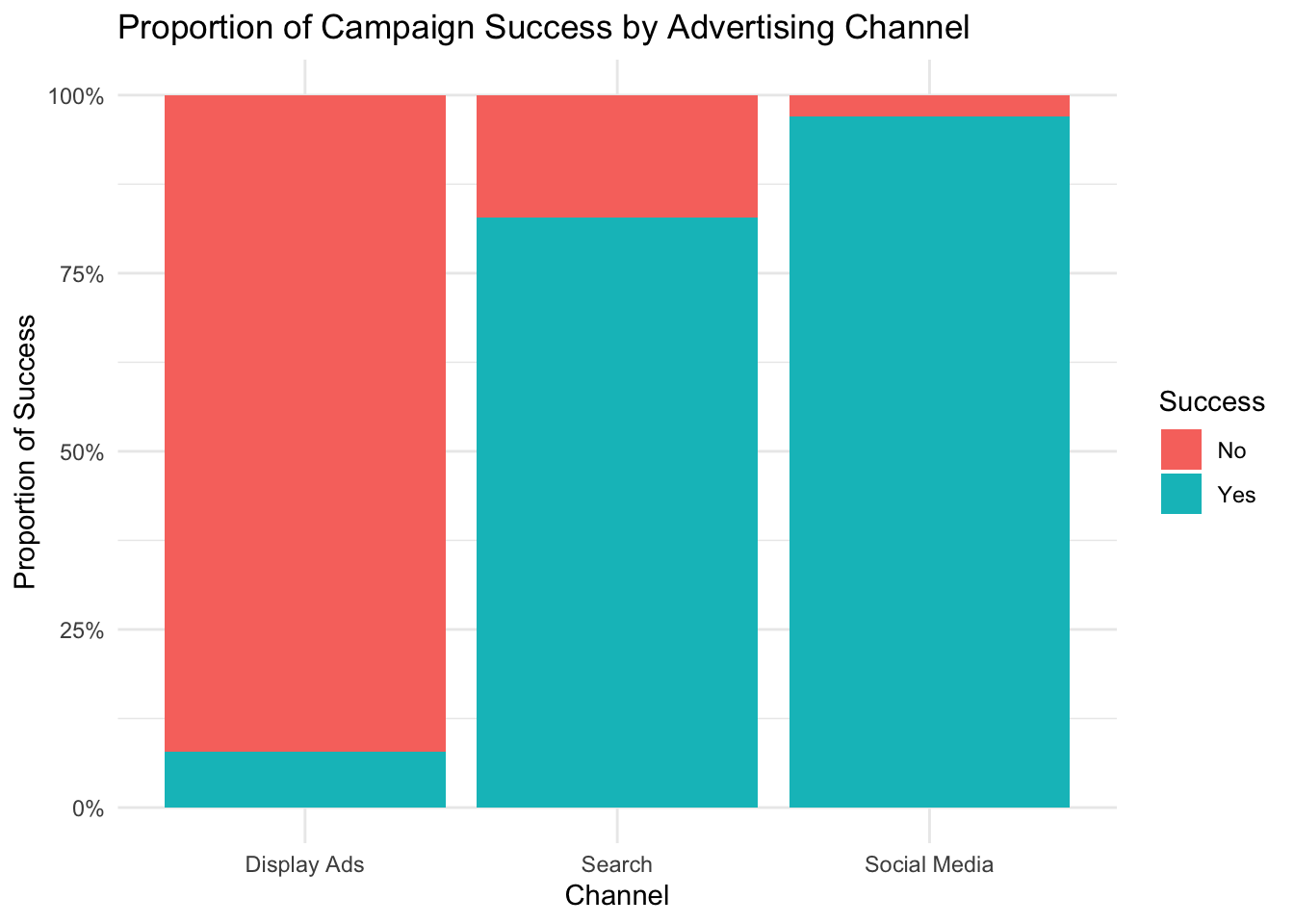

In this chart, each bar represents a channel, and the colors within each bar show the proportion of successful vs. unsuccessful campaigns. This helps us quickly assess if certain channels tend to have higher success rates.

Mosaic Plots

A mosaic plot is a graphical representation of contingency tables. It shows the proportion of each combination of categories by dividing a rectangle into tiles, with each tile’s area proportional to the frequency or count of observations in that category combination.

When to Use a Mosaic Plot

Mosaic plots are particularly useful when you want to:

  • Visualize associations between two categorical variables.
  • Understand proportions and patterns within a dataset without exact counts.
  • See if categories of one variable are evenly or unevenly distributed across levels of another variable.

For example, in AdBoost’s marketing_data, we could create a mosaic plot to show the relationship between channel and success.

Creating a Mosaic Plot

We’ll use the vcd package, which is designed for visualizing categorical data, to create the mosaic plot. If you haven’t installed vcd yet, you can do so by running:

# install the vcd package if necessary
#install.packages("vcd")

Once the package is installed, you can create a mosaic plot with the following code:

# Load the vcd package
library(vcd)

# Create a mosaic plot for 'channel' and 'success'
mosaic(~ channel + success, data = marketing_data,
       shade = TRUE, legend = TRUE,
       main = "Mosaic Plot of Channel and Success")

Explanation of the Code

  • ~ channel + success: This formula specifies the two categorical variables (channel and success) for the mosaic plot.
  • data = marketing_data: Specifies the dataset.
  • shade = TRUE: Adds color shading to the plot to indicate deviations from independence.
  • legend = TRUE: Adds a legend to the plot, helping interpret the shading.
  • main: Provides a title for the plot.

Interpreting the Mosaic Plot

  1. Tile Sizes: Each rectangle in the plot represents a unique combination of channel and success. The area of each tile is proportional to the frequency of observations for that combination. For instance, a larger tile indicates a more common combination, while a smaller tile represents a less frequent combination.

  2. Shading: With shade = TRUE, colors are used to highlight significant deviations from independence:

    • Darker or brighter colors indicate larger deviations, meaning that the observed counts are much higher or lower than expected if channel and success were independent.
    • Neutral colors (close to white) suggest that the observed counts are close to what we’d expect under independence.

  3. Patterns in the Data: By examining the size and shading of the tiles, you can infer relationships between channel and success:

    • If certain channel categories consistently appear with “Yes” or “No” in success, this will show up in the plot as larger and possibly shaded tiles, indicating a non-random pattern.
    • In contrast, if the tiles are roughly equal in size and neutral in color, it suggests there may be little association between channel and success.

This plot offers an easy-to-understand visual summary of how success rates differ by channel, which can be more informative than simply looking at raw numbers in a table.

Exercise: Categorical-Categorical Analysis with MetroMart

Try it yourself:

In this exercise, you’ll use the sales_data dataset from MetroMart to explore relationships between categorical variables.

Quick Data Recap

Here are the key variables you’ll work with:

  • Region: The region where each sale occurred (North, South, East, or West).
  • Promotion: Whether the product was on promotion (Yes or No).
  • Category: Product category (Electronics, Grocery, Clothing, or Home Goods).

Using the MetroMart dataset, answer the following questions:

  1. Create a Contingency Table: Generate a contingency table to show the frequency of each combination of region and promotion.

  2. Chi-Square Test for Independence: Conduct a chi-square test to check if promotion is independent of region.

  3. Visualize the Relationship: Create a stacked bar chart of promotion within each region.

  4. Exploring Category and Promotion: Generate another stacked bar chart of promotion within each category.

Hint 1

  1. Perform the ANOVA test of price across categories. Then, if the ANOVA test shows significant differences, perform the TukeyHSD test. Then generate a box plot of price across categories

  2. Perform the t-test of quantity sold across promotion status. Then generate a box plot of quantity sold across promotion status

  3. Generate a box plot of quantity sold across categories

  4. Generate a box plot of price across promotion status split across categories (hint in a hint: consider facet_grid() for creating another layer of splitting)

Hint 2

  1. ANOVA of price across categories

    1. Call the aov() function specifying the numeric variable (price) as the y variable and the categorical variable (category) as the x variable
    2. If the ANOVA test is significant, call the TukeyHSD() function specifying the ANOVA results as the input
    3. Call the ggplot() function, specify the data as sales_data, map the aesthetic with x = category and y = price specify the geometry as `geom_boxplot()

  2. Analyzing the Impact of Promotions on Quantity Sold

    1. Call the t.test() function specifying data as sales_data, quantity_sold (numeric variable) as the y-variable and promotion (categorical variable) as the x variable
    2. Call the ggplot() function, specify the data as sales_data, map the aesthetic with x = promotion and y = quantity_sold, specify the geometry as `geom_boxplot()

  3. Exploring Sales Patterns Across Categories

    1. Call the ggplot() function, specify the data as sales_data, map the aesthetic with x = category and y = quantity_sold, specify the geometry as `geom_boxplot()

  4. Combining Category and Promotion to Examine Price Sensitivity

    1. Call the ggplot() function, specify the data as sales_data, map the aesthetic with x = promotion and y = price, specify the geometry as `geom_boxplot(), specify facet_grid as category; OR
    2. Create a new promo_category variable that combines promotion and category, call the ggplot() function, specify the data as sales_data, map the aesthetic with x = promo_category and y = price, specify the geometry as `geom_boxplot()

Fully worked solution:

# 1. Generate a contingency table for 'region' and 'promotion'
table(sales_data$region, sales_data$promotion)  

# 2. # Perform chi-square test for independence between 'promotion' and 'region'
chisq.test(table(sales_data$region, sales_data$promotion))

# 3. # Stacked bar chart of promotion within each region
ggplot(sales_data, aes(x = region, fill = promotion)) +
  geom_bar(position = "fill") +
  labs(
    title = "Proportion of of Products on Promotion  by Region",
    x = "Region",
    y = "Proportion of Products on Promotion",
    fill = "Promotion"
  ) +
  scale_y_continuous(labels = scales::percent) +
  theme_minimal()
  
# 4. # Generate another stacked bar chart of promotion within each category.  
ggplot(sales_data, aes(x = category, fill = promotion)) +
  geom_bar(position = "fill") +
  labs(
    title = "Proportion of of Products on Promotion by Category",
    x = "Region",
    y = "Proportion of Products on Promotion",
    fill = "Promotion"
  ) +
  scale_y_continuous(labels = scales::percent) +
  theme_minimal()

  1. Create a Contingency Table: What patterns do you observe in the distribution as revealed in the contingency table?

  2. Chi-Square Test for Independence: Based on the p-value of the chi-square, can you conclude that there’s an association between promotion status and region?

  3. Visualize the Relationship: Does the visualization of the stacked bar chart reveal any trends in promotion distribution across regions?

  4. Exploring Category and Promotion: Based on the stacked bar chart of promotion within each category, what do you observe about the proportion of promoted products across categories?

Summarize your findings from the chi-square test and visualizations. Based on the results, what insights could MetroMart gain regarding how promotions vary by region or product category? How might this inform their marketing and promotional strategies?

24.5 Chapter Summary: Bivariate Exploratory Data Analysis

In this chapter, we explored the foundations of Bivariate Exploratory Data Analysis (EDA), focusing on methods to investigate relationships between pairs of variables. Bivariate EDA provides entrepreneurs and analysts with valuable insights into how variables interact, informing strategic decisions.

Key techniques included:

  • Numeric-Numeric Analysis: We used scatter plots with trend lines, along with covariance and correlation measures, to understand how pairs of numeric variables relate. These tools help reveal trends, associations, and the strength of relationships between variables like advertising spend and revenue.

  • Numeric-Categorical Analysis: By applying statistical tests such as t-tests and ANOVA, and using visualizations like box plots, we examined how numeric outcomes (e.g., quantity sold) vary across categories (e.g., promotion status). This analysis helps businesses understand how categories influence outcomes, assisting in areas like pricing and targeted promotions.

  • Categorical-Categorical Analysis: Using contingency tables, chi-square tests, and mosaic plots, we explored relationships between pairs of categorical variables. This analysis sheds light on associations, such as how different regions respond to promotions, which can guide marketing strategies and inventory management.

Bivariate EDA empowers businesses to uncover actionable patterns and test hypotheses about variable relationships. By combining statistical summaries with visualizations, entrepreneurs can make data-driven decisions that enhance marketing, operations, and strategic planning. This chapter has equipped you with foundational techniques to analyze variable pairs effectively, setting the stage for more advanced modeling and predictive analysis.

  1. A monotonic relationship is a type of relationship between two variables where, as one variable increases, the other variable either consistently increases or consistently decreases.↩︎