# A tibble: 100 × 4
age spending product_interest region
<dbl> <dbl> <chr> <chr>
1 33 495 Fashion East
2 18 458 Fashion North
3 32 491 Health South
4 30 420 Fashion South
5 85 664 Fashion East
6 35 533 Fashion East
7 31 526 Health South
8 14 350 Fashion South
9 24 471 Health East
10 NA 424 Fashion South
# ℹ 90 more rows27 Univariate EDA: Statistics
Numerical quantities focus on expected values, graphical summaries on unexpected values.— John Tukey
27.1 Introduction
Univariate Exploratory Data Analysis (EDA) examines individual variables to understand their characteristics, assess data quality, and uncover insights. While visualization offers a powerful first step in identifying patterns and anomalies, statistical measures provide the precision needed to quantify those findings. For entrepreneurs, statistical analysis of univariate data helps in setting benchmarks, interpreting trends, and making informed decisions based on key metrics.
Univariate statistical EDA involves three core steps:
- Descriptive Statistics: Use measures like mean, median, and mode to understand central tendencies and variability.
- Data Quality Assessment: Employ statistics to detect missing data, duplicates, and outliers that could affect analysis.
- Advanced Analysis: Apply tools like skewness, kurtosis, and normality tests to deepen your understanding of variable behavior.
As outlined in Exploring Data, this structured approach to EDA ensures that each variable is thoroughly analyzed before proceeding to more complex multivariate relationships. In this chapter, we’ll focus on statistical techniques for univariate EDA, building on the visual exploration methods introduced in Chapter 26. Together, these tools will provide a comprehensive understanding of your data and prepare it for deeper analysis.
27.2 Demonstration Data: UrbanFind
In this chapter, we revisit the UrbanFind dataset to explore its statistical properties and how they can guide actionable insights. UrbanFind is a startup curating personalized recommendations for city dwellers, focusing on four key product categories:
- Tech Gadgets: Modern devices and tools enhancing urban living.
- Fashion: Stylish and functional apparel and accessories.
- Outdoor Activities: Gear and ideas for accessible urban adventures.
- Health and Wellness: Products aimed at improving personal well-being.
The dataset, introduced in Section 26.3, provides a foundation for analyzing individual variables to understand customer demographics, spending habits, and preferences.
Variables in UrbanFind’s Data
UrbanFind’s survey captured key data points to inform their strategy:
- Age: A customer’s age in years, which influences preferences across product categories.
- Spending: The amount spent (in dollars) on lifestyle products in the past month, indicating purchasing power and habits.
- Product Interest: The customer’s favorite product category among Tech, Fashion, Outdoors, and Health.
- Region: The geographic location of each customer, categorized into North, South, East, or West, which highlights regional variations in preferences.
Each variable offers a unique perspective on UrbanFind’s customer base, providing valuable insights for targeted marketing and product development.
Purpose of the UrbanFind customer_data Dataset
In this chapter, we’ll delve into the statistical characteristics of these variables to answer critical questions:
- What are the typical (mean or median) values, and how do they vary?
- Are there any extreme or unusual values (outliers)?
- How are patterns in individual variables aligned with UrbanFind’s business strategy?
By applying descriptive statistics, we’ll quantify key attributes of UrbanFind’s customer data, deepening the understanding built through visualization.
Preview of the UrbanFind customer_data Dataset
Here’s a snapshot of the customer_data dataset, offering a glimpse of the variability and structure in the data.
For a more detailed introduction to the dataset, refer to Chapter 26.
27.3 Descriptive Statistics
Descriptive statistics provide a concise summary of your data and offer insights into its distribution, central tendencies, and variability. We’ll start with R’s summary() function to get a high-level overview, then calculate more specific measures with individual functions. In this section, we’ll calculate these key statistics to get a comprehensive understanding of the customer_data dataset from UrbanFind.
Summary Statistics with summary()
R’s summary() function provides a quick overview of key statistics, including measures of central tendency and spread (e.g., mean, median, and range). This overview often reveals initial insights, including potential outliers and data skewness.
# Summary statistics for customer_data
summary(customer_data) age spending product_interest region
Min. :14.00 Min. : 139.0 Length:100 Length:100
1st Qu.:29.00 1st Qu.: 431.2 Class :character Class :character
Median :37.00 Median : 529.0 Mode :character Mode :character
Mean :36.81 Mean : 543.8
3rd Qu.:43.00 3rd Qu.: 627.8
Max. :90.00 Max. :1600.0
NA's :3 NA's :2 The summary() function outputs the mean and median for continuous variables like age and spending and also shows the minimum and maximum values (range). However, it doesn’t cover standard deviation or interquartile range (IQR) directly, which we’ll calculate separately.
From the summary(), we see that the mean age is 36.81 and the median age is 37 which are close in value. We also see that the mean spending of $543.83 and median spending of $529 are close in value.
Interpretation: When the mean and median are similar, as seen here for both customer
ageandspending, it suggests a balanced, symmetrical distribution with minimal skew. To determine how closely values cluster around the average, we also need to examine the range and standard deviation.
Measures of Central Tendency
Central tendency indicates the “typical” or “average” values within the data, helping us understand what’s most representative. Let’s calculate these measures with R functions to see how they differ and when each is most useful.
Mean
The mean is the average value, which is useful for understanding overall levels. However, it can be influenced by outliers.
# Calculate mean for age and spending
mean(customer_data$age, na.rm = TRUE)[1] 36.81443mean(customer_data$spending, na.rm = TRUE)[1] 543.8265Median
The median represents the middle value, which can be more informative than the mean for skewed distributions, as it’s less affected by outliers.
# Calculate median for age and spending
median(customer_data$age, na.rm = TRUE)[1] 37median(customer_data$spending, na.rm = TRUE)[1] 529Mode
The mode is the most frequently occurring value, especially useful for categorical data. For example, let’s calculate the mode for product_interest in customer_data.
# Calculate mode for product_interest
table(customer_data$product_interest)
Fashion Health Outdoors Tech
25 24 27 22 table(customer_data$product_interest) |> which.max()Outdoors
3 Measures of Spread
While measures of central tendency (like mean and median) give us an idea of typical values, measures of spread reveal how much the data varies around those central values. Understanding the spread is essential for interpreting data patterns, as it tells us whether values are tightly clustered around the mean or widely dispersed. For instance, high variability suggests diverse customer profiles, while low variability indicates uniformity.
Here, we’ll explore three key measures of spread: range, standard deviation, and variance. Each provides a unique perspective on data variability.
Range
The range is the difference between the maximum and minimum values. It’s simple but can be affected by outliers.
# Calculate range for age and spending
range(customer_data$age, na.rm = TRUE)[1] 14 90range(customer_data$spending, na.rm = TRUE)[1] 139 1600In customer_data, the range of age is from 14 to 90, while the range of spending spans from $139 to $1600. These ranges show the full spectrum of prices and quantities but don’t tell us how common values are within this span.
Interquartile Range (IQR)
The IQR measures the spread of the middle 50% of values and is particularly useful for understanding spread in skewed data. It’s calculated as the difference between the 75th percentile (75% of values fall below this point) and 25th percentile (25% of values fall below this point):
\[ \mathsf{IQR = Q3 - Q1}.\]
# Calculate IQR for age and spending
IQR(customer_data$age, na.rm = TRUE)[1] 14IQR(customer_data$spending, na.rm = TRUE)[1] 196.5The IQR of age is 14, meaning the middle 50% of prices fall within this range. For spending, the IQR is $196.5.
The IQR is especially useful in box plots, where it represents the range of the central box.
Standard Deviation (SD)
The standard deviation measures the average distance of each value from the mean. A low SD indicates that values are clustered near the mean, while a high SD suggests more variability. Standard deviation is useful for interpreting consistency in data.
# Calculate standard deviation for age and spending
sd(customer_data$age, na.rm = TRUE)[1] 13.2534sd(customer_data$spending, na.rm = TRUE)[1] 207.0577The standard deviation for customer age is 13.25, and for spending, it’s $207.06. These values show how much age and purchasing typically vary from their respective means.
Interpretation: Measures of spread are crucial for understanding data variability. For example, a low standard deviation in customer ages could imply a relatively homogenous customer segment that can be reached through the same channels while a higher standard deviation in spending might indicate diverse customer income levels or buying patterns. Understanding variability helps UrbanFind plan for advertising, inventory, and fluctuations in sales.
Exercise: Calculating Descriptive Statistics
Try it yourself:
The sales_data dataset represents a set of sales records for a fictional company named MetroMart, which operates across multiple regions. This dataset was created to demonstrate descriptive statistics and data exploration techniques, essential for understanding product performance and sales trends.
We’ll work with both continuous variables (e.g., price, quantity_sold) and categorical variables (e.g., region, category, and promotion).
Dataset Overview:
- Product ID: A unique identifier for each product (from 1 to 300).
- Price: The selling price of each product, normally distributed with a mean price of $20 and some variation to represent typical pricing diversity.
- Quantity Sold: The number of units sold, following a Poisson distribution to reflect typical purchase quantities.
- Region: The region where each product was sold, categorized into North, South, East, and West regions.
- Category: The product category, which can be one of four types: Electronics, Grocery, Clothing, or Home Goods. This variable helps us understand which product types tend to perform better in terms of sales volume and pricing across different regions.
- Promotion: Indicates whether the product was on promotion at the time of sale, with possible values of “Yes” or “No.” This variable allows us to analyze how promotional offers affect sales volume and may reveal seasonal or regional preferences for discounted products.
This provides a rich foundation for exploring key statistical concepts, such as central tendency and variability, while allowing us to analyze categorical differences. With these variables, we can gain insights into average prices, sales volume, and how factors like product type, regional differences, and promotions influence sales. These metrics can reveal patterns, outliers, and trends that are crucial for strategic decision-making in areas such as pricing, inventory management, and targeted marketing.
For MetroMart’s sales_data:
Calculate the measures of central tendency (mean and median) for the
priceandquantity_soldvariables to understand the typical values for these sales metrics.Calculate the mode of the categorical variables, such as
region, to see where most purchases happen, andcategoryto identify the most popular product type.Calculate the spread of the
priceandquantity_soldvariables to understand how they differ from their means, and analyze howpromotionmight influence these values.
Hint 1
- Calculate descriptive statistics for mean and median using the
summary()function.
- Calculate the mode of the categorical variables using
table() - Calculate descriptive statistics for spread (range, IQR, and standard deviation) using the appropriate R functions.
Hint 2
For descriptive statistics about central tendencies:
- Call the
summary()function - Specify the data as
sales_data
- Call the
For descriptive statistics about spread:
- Call the
range()function forsales_dataand thepriceandquantity_soldvariables – be sure to removeNAvalues from the calculation - Call the
IQR()function forsales_dataand thepriceandquantity_soldvariables – be sure to removeNAvalues from the calculation - Call the
sd()function forsales_dataand thepriceandquantity_soldvariables – be sure to removeNAvalues from the calculation
- Call the
summary()
range()
IQR()
sd() Fully worked solution:
1summary(sales_data)
2table(sales_data$region)
table(sales_data$category)
table(sales_data$promotion)
3range(sales_data$price, na.rm = TRUE)
range(sales_data$quantity_sold, na.rm = TRUE)
4IQR(sales_data$price, na.rm = TRUE)
IQR(sales_data$quantity_sold, na.rm = TRUE)
5sd(sales_data$price, na.rm = TRUE)
sd(sales_data$quantity_sold, na.rm = TRUE)- 1
-
Call the
summary()function forsales_data - 2
-
Call the
table()function for categorical variablesregion,category, andpromotion. - 3
-
Call the
range()function forsales_dataand thepriceandquantity_soldvariables removingNAvalues from the calculation - 4
-
Call the
IQR()function forsales_dataand thepriceandquantity_soldvariables removingNAvalues from the calculation - 5
-
Call the
sd()function forsales_dataand thepriceandquantity_soldvariables removingNAvalues from the calculation
- Compare mean and median to see if the data may be skewed.
- What does the spread of the data suggest about the diversity of prices? quantity sold?
In exploring any dataset, descriptive statistics provide a foundation for understanding key characteristics of the data. They allow us to summarize central tendencies, variations, and identify any unusual patterns that may be present.
27.4 Detecting Outliers
Whenever I see an outlier, I never know whether to throw it away or patent it.– Bert Gunter (2015)
In Chapter 16 Inspect Data, we introduced data quality assessment, exploring how to detect missing data, duplicates, and outliers. That chapter provided high-level strategies for recognizing potential outliers using summary statistics (e.g., minimum and maximum values), visualizations (e.g., box plots), and categorical frequencies. We also discussed practical guidelines for when to address or retain outliers, emphasizing the importance of understanding their context and potential value.
Now, we turn to more advanced statistical methods for detecting outliers. These methods allow us to systematically identify data points that deviate significantly from others in a dataset, helping to distinguish between data entry errors, anomalies, or meaningful variations that could inform insights.
Outliers play a dual role in data analysis: they can distort statistical measures like the mean and variance or provide valuable information about rare but important phenomena. In Exploratory Data Analysis (EDA), careful outlier detection is critical to ensuring both the quality and interpretability of results.
In this section, we’ll explore several techniques for detecting outliers, starting with Tukey’s interquartile range (IQR) method and moving to Z-scores, box plots, and guidance on selecting the most appropriate method for your analysis. Each approach offers unique strengths, depending on the data’s structure and the goals of the analysis.
Testing for Outliers with Interquartile Range (IQR)
The IQR method is useful for data that is not normally distributed. This method defines outliers as values that fall below \(\mathsf{Q1 - 1.5 \cdot IQR}\) or above \(\mathsf{Q3 + 1.5 * IQR}\).
Demonstration of the IQR Test
# Calculate IQR and define bounds for potential outliers
q1 <- quantile(sales_data$price, 0.25, na.rm = T) # calculate the first quantile
q3 <- quantile(sales_data$price, 0.75, na.rm = T) # calculate the third quantile
iqr <- q3 - q1 # calculate iqr
# Define lower and upper bounds for outliers
lower_bound <- q1 - 1.5 * iqr # define the lower bound
upper_bound <- q3 + 1.5 * iqr # define the upper bound
# Filter potential outliers based on IQR bounds
iqr_outliers <- sales_data %>% filter(price < lower_bound | price > upper_bound)
iqr_outliers product_id price quantity_sold region
1 156 5.88 22 NorthUsing the IQR calculation, we can conclude that there is one outlier in the price variable from sales_data, namely the observation of product_id = 156. Notice that the Z-score for this observation is meaning that the Z-score was also close to identifying this observation as an outlier.
The IQR method is especially effective for detecting outliers in skewed data, as it isn’t influenced by extreme values on either end.
Testing for Outliers with Z-Scores
When data is approximately normal, we can use Z-scores to tell us how many standard deviations a value is from the mean. Values that are more than ±2 standard deviations from the mean may be considered unusual. Values that are more than ±3 standard deviations from the mean are usually classified as outliers.
Z-score: A Z-score tells us how many standard deviations an observed value (\(\mathsf{X}\)) is from the mean (\(\mathsf{\mu}\)):
\[ \mathsf{Z = \dfrac{X - \mu}{\sigma}} \]
where \(\mathsf{X}\) is the observed value, \(\mathsf{\mu}\) is the mean, and \(\mathsf{\sigma}\) is the standard deviation.
The following plot illustrates the concept of Z-scores on a normal distribution, with dashed lines at ±2 standard deviations and dotted lines at ±3 standard deviations to mark the bounds of “usual” and “outlier” values.
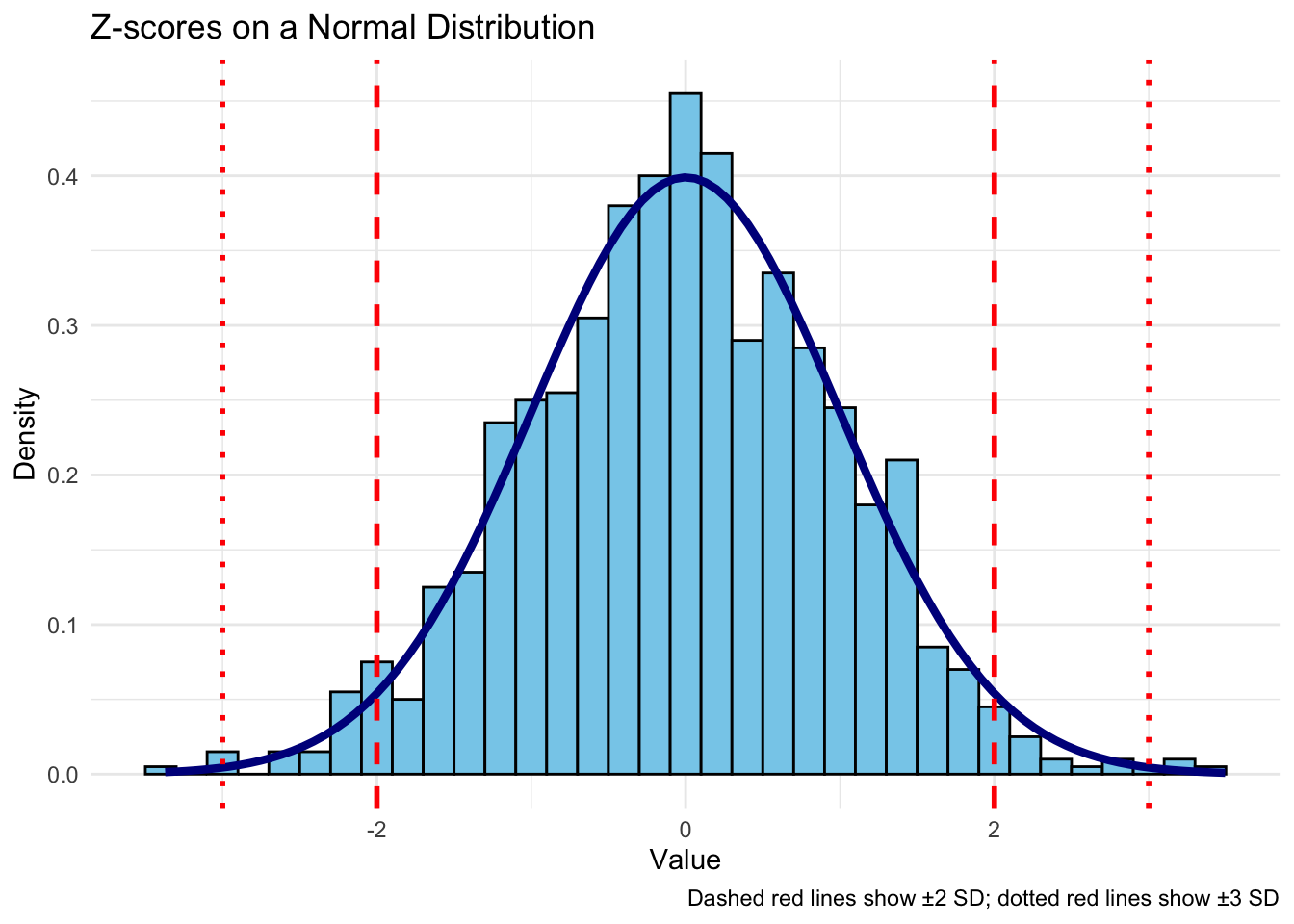
In this plot, the dashed red lines at ±2 standard deviations and the dotted red lines at ±3 standard deviations illustrate where values are likely to be considered unusual or outliers based on their Z-scores.
Demonstration of the Z-score Test
To test for outliers with Z-scores in our sales_data dataset, we’ll calculate the Z-scores for the price variable and check for any values that are more than 3 standard deviations from the mean. Here’s how it’s done in R:
# Calculate Z-scores for sales_data
sales_data$z_score_price <- (sales_data$price -
mean(sales_data$price, na.rm = TRUE)) /
sd(sales_data$price, na.rm = TRUE)
# Filtering potential outliers based on Z-scores
z_score_outliers <- sales_data %>% filter(abs(z_score_price) > 3)
z_score_outliers[1] product_id price quantity_sold region z_score_price
<0 rows> (or 0-length row.names)In this example, we check the price variable for outliers. If z_score_outliers returns zero rows, we can conclude that there are no outliers in the price variable of sales_data.
Note: Z-scores assume a normal distribution. For non-normal distributions, consider other outlier detection methods, such as the IQR-based method
Testing for Outliers with Box Plots
A box plot visually identifies outliers as individual points beyond the whiskers. In a standard box plot, whiskers extend up to 1.5 times the IQR. Points beyond this range are considered potential outliers.
Demonstration of the Box Plot Test
# Box plot to visually identify outliers in price
ggplot(sales_data, aes(x = "", y = price)) +
geom_boxplot(outlier.color = "red", outlier.shape = 16) +
labs(title = "Box Plot of Product Prices with Outliers Highlighted", y = "Price") +
theme_minimal()
This box plot clearly identifies a single value, the minimum value, of price as an outlier. Checking the data we can verify that the lowest price in sales_data is the observation for product_id = 156.
# slice and display the observation (row) with minimum price
sales_data |> slice_min(price) product_id price quantity_sold region z_score_price
1 156 5.88 22 North -2.990809Choosing an Outlier Detection Method
The best method depends on the data distribution and the context of analysis:
- Z-scores are suitable for normally distributed data.
- IQR is robust and works well with skewed data.
- Box plots provide a quick, visual approach for outlier detection for any shape of distribution.
Takeaway: Detecting outliers helps identify unusual or potentially erroneous data points. By carefully assessing outliers, we can refine data quality and uncover valuable insights for analysis and decision-making.
Each method offers different insights, making it beneficial to combine them for a comprehensive approach to outlier detection.
Exercise: Testing for Outliers with Statistics and Visalization
Try it yourself:
Perform the Z-score, IQR, and box plot tests to determine whether the age and/or spending variables in UrbanFind’s customer_data have outliers. Which test is more appropriate?
Hint 1
- Calculate the Z-score and the IQR test score for both variables.
- Visualize the box plot for both variables.
Hint 2
For Z-scores:
- Calculate (age - mean(age)) / sd(age)
- Calculate (spending - mean(spending)) / sd(spending)
- Filter the data to identify cases where the Z-score is more than 3 standard deviations from the variable value
(variable - mean(variable)) / sd(variable)
data |> filter (abs(z_score) > 3)For the IQR test
- Calculate the IQR test values Q1 - 1.5 * IQR and Q3 + 1.5 * IQR for age
- Calculate the IQR test values Q1 - 1.5 * IQR and Q3 + 1.5 * IQR for spending
- Filter the data to identify cases where the value of an observation is less than the lower bound or greater than the upper bound
# Calculate quantiles and IQR
q1 <- quantile(variable, 0.25)
q3 <- quantile(variable, 0.75)
iqr <- q3 - q1
# Define lower and upper bounds for outliers
lower_bound <- q1 - 1.5 * iqr
upper_bound <- q3 + 1.5 * iqr
# Filter potential outliers based on IQR bounds
data |> filter(variable < lower_bound | variable > upper_bound)For the box plot test
- Plot the box plot for age and for spending
- Visually check for outliers
- Filter or slice to identify the observations with outliers
ggplot(data, aes(x = "", y = variable)) +
geom_boxplot()
data |> slice_min(order_by = variable, n = number_of_outliers)
data |> slice_max(order_by = variable, n = number_of_outliers)
filter(condition) Fully worked solution:
1customer_data$z_score_age <- (customer_data$age - mean(customer_data$age, na.rm = T)) / sd(customer_data$age, na.rm = T)
customer_data |> filter(abs(z_score_age) > 3)
##
customer_data$z_score_spending <- (customer_data$spending - mean(customer_data$spending, na.rm = T)) / sd(customer_data$spending, na.rm = T)
customer_data |> filter(abs(z_score_spending) > 3)
2q1 <- quantile(customer_data$age, 0.25, na.rm = T)
q3 <- quantile(customer_data$age, 0.75, na.rm = T)
iqr <- q3 - q1
lower_bound <- q1 - 1.5 * iqr
upper_bound <- q3 + 1.5 * iqr
customer_data %>% filter(age < lower_bound | age > upper_bound)
#
q1 <- quantile(customer_data$spending, 0.25, na.rm = T)
q3 <- quantile(customer_data$spending, 0.75, na.rm = T)
iqr <- q3 - q1
lower_bound <- q1 - 1.5 * iqr
upper_bound <- q3 + 1.5 * iqr
customer_data %>% filter(spending < lower_bound | spending > upper_bound)
ggplot(customer_data, aes(x = "", y = age)) +
3 geom_boxplot(outlier.color = "red", outlier.shape = 16)
customer_data |> slice_max(order_by = age, n = 2)
#
ggplot(customer_data, aes(x = "", y = spending)) +
geom_boxplot(outlier.color = "red", outlier.shape = 16)
customer_data |> slice_max(order_by = spending, n = 2)
customer_data |> slice_max(order_by = spending, n = 1) - 1
- Calculate the Z-score and filter for observations greater than 3 standard deviations.
- 2
- Calculate the IQR upper- and lower-bounds and filter for observations above or below them.
- 3
- Plot the box plot, visually check for outliers, filter/slice the outliers
- What observations may be outliers?
- Which test seems more appropriate to test for outliers in these variables?
27.5 Skewness and Kurtosis
Measuring Skewness and Kurtosis
Skewness and kurtosis describe the shape of a variable’s distribution, providing insight into asymmetry (skewness) and the presence of heavy tails or peakedness (kurtosis). These concepts are foundational to understanding how data deviates from a normal distribution and are explored further in Univariate EDA: Statistics.
Skewness
Skewness measures the asymmetry of a distribution:
- Positive skew: The tail on the right side is longer (e.g., income distributions with a few high earners).
- Negative skew: The tail on the left side is longer (e.g., datasets with minimum thresholds, like age of retirement).
Formula:
\[ \mathsf{Skewness} = \mathsf{\frac{\frac{1}{n} \sum_{i=1}^n (x_i - \bar{x})^3}{\sigma^3}} \]
Kurtosis
Kurtosis measures the “tailedness” (thickness of the tails) of a distribution:
- High kurtosis (leptokurtic): Indicates more extreme values (e.g., stock returns during volatile markets).
- Low kurtosis (platykurtic): Indicates fewer extreme values.
Formula: \[ \mathsf{Kurtosis} = \mathsf{\frac{\frac{1}{n} \sum_{i=1}^n (x_i - \bar{x})^4}{\sigma^4} - 3} \]
Calculating Skewness and Kurtosis in R
Use the moments package for quick calculations:
# Install moments package if needed
#if (!require(moments)) install.packages("moments")
# Example calculations
library(moments)
skewness_value <- skewness(customer_data$spending, na.rm = TRUE)
kurtosis_value <- kurtosis(customer_data$age, na.rm = TRUE)
skewness_value[1] 2.323303kurtosis_value[1] 5.994014Hypothesis Testing for Skewness and Kurtosis
Testing Skewness
The D’Agostino test evaluates whether a dataset is symmetric (skewness = 0). Use the agostino.test() function from the moments package.
Testing Kurtosis
The Anscombe-Glynn test assesses whether the kurtosis matches that of a normal distribution (kurtosis = 0). Use the anscombe.test() function.
Practical Implications for Entrepreneurship
Understanding skewness and kurtosis allows entrepreneurs to:
- Identify extreme cases (e.g., top customers or risky products).
- Segment markets with distinct variability patterns.
- Adjust pricing strategies based on customer behavior.
Example Interpretation
- High skewness (positive): A small number of high-value products may dominate sales.
- High kurtosis: A few customers or transactions might account for extreme values.
Demonstration: Measuring and Testing Skewness and Kurtosis
Let’s analyze the spending variable in ecommerce_data:
# Calculate skewness and kurtosis
spending_skewness <- skewness(customer_data$spending, na.rm = TRUE)
spending_kurtosis <- kurtosis(customer_data$spending, na.rm = TRUE)
# Perform hypothesis tests
library(moments)
agostino_test <- agostino.test(customer_data$spending)
anscombe_test <- anscombe.test(customer_data$spending)
#jarque_test <- jarque.test(customer_data$spending)
list(
Skewness = spending_skewness,
Kurtosis = spending_kurtosis,
Agostino_Test = agostino_test$p.value,
Anscombe_Test = anscombe_test$p.value#,
# Jarque_Bera_Test = jarque_test$p.value
)$Skewness
[1] 2.323303
$Kurtosis
[1] 12.79021
$Agostino_Test
[1] 6.700545e-11
$Anscombe_Test
[1] 6.22492e-08Discuss the results in terms of their implications for UrbanFind’s pricing strategies or customer segmentation.
The table below outlines essential descriptive statistics techniques, each providing unique insights into different aspects of a dataset.
| Measure | Description | Continuous | Categorical |
|---|---|---|---|
| Central Tendency | Measures the “typical” value | ✅ (Mean, Median) | ✅ (Mode) |
| Variation | Measures data spread | ✅ (Range, SD, IQR) | ❌ |
| Skewness & Kurtosis | Assesses data symmetry and tail heaviness | ✅ (Skewness, Kurtosis) | ❌ |
| Outlier Detection | Identifies unusual values using thresholds | ✅ (Z-score, IQR) | ❌ |
| Normality Tests | Tests if data follows a normal distribution | ✅ (Shapiro-Wilk) | ❌ |
27.6 Interpretation in Entrepreneurship
Understanding distribution shape allows us to make better data-driven decisions:
- Detecting Skew: Skewness tells us if a variable’s distribution leans towards higher or lower values. For instance, if product prices are right-skewed, most products are affordable, but a few are premium-priced.
- Identifying Outliers: Box plots make it easy to spot outliers. Outliers could indicate data errors or valuable insights, like a product that sells exceptionally well or poorly.
- Assessing Variability: Histograms and box plots help in quickly visualizing data spread, giving insight into whether values cluster tightly around the mean or are widely dispersed.
By combining histograms, box plots, and an understanding of skewness and kurtosis, we gain a clearer view of data characteristics, which aids in further analysis and informs decision-making.
27.7 Practical Workflow for Univariate EDA
Exploratory Data Analysis (EDA) is an iterative process that blends curiosity, critical thinking, and technical skills to understand and prepare data for analysis. For univariate EDA, the process involves systematically examining each variable in a dataset to ensure data quality, uncover patterns, and identify potential challenges.
The following practical workflow outlines a structured approach to univariate EDA:
- Begin with Integrity: By addressing missing and duplicate data first, you establish a clean and trustworthy dataset for analysis.
- Explore with Visualization: Visualizations provide an immediate, intuitive understanding of the data’s shape and patterns.
- Quantify with Statistics: Descriptive statistics give precise measures of central tendency and variability to support findings from visual exploration.
- Spot the Unusual: Detecting and understanding outliers ensures that potential anomalies are addressed appropriately, whether they represent errors or valuable insights.
By following these steps, you can confidently navigate univariate EDA, ensuring the data is ready for deeper analysis and actionable insights. This methodical process lays the groundwork for effective data-driven decision-making.
Step 1: Identify Missing and Duplicate Data
Before diving into distributions or patterns, it’s crucial to ensure the dataset’s integrity. Missing or duplicate data can distort analysis and lead to misleading conclusions.
- Why it matters: Missing values may indicate errors in data collection or provide meaningful information about the dataset’s context (e.g., non-responses in surveys). Duplicate entries can inflate counts, skew averages, and affect statistical inferences.
- What to do: Use tools like
is.na(),skimr::skim(), orjanitor::get_dupes()to quickly identify and quantify missing and duplicate data. This step sets the foundation for all subsequent analysis by ensuring the dataset is complete and reliable.
Step 2: Visualize Distributions Using Histograms, Box Plots, and Bar Plots
Visualization is often the first lens through which we explore data. By plotting variables, we can uncover patterns, anomalies, and key characteristics that might not be evident in raw data.
- Why it matters: Visualizing distributions provides an intuitive understanding of the data’s shape, spread, and unusual values. Histograms reveal clustering and skewness, box plots highlight spread and outliers, and bar plots showcase categorical distributions.
- What to do: Start by creating histograms for continuous variables to assess the distribution’s overall shape. Use box plots to identify outliers and understand variability. For categorical variables, bar plots offer a clear picture of frequency counts across categories.
Step 3: Summarize Variables with Descriptive Statistics
While visualizations offer a qualitative view, descriptive statistics provide quantitative insights into a variable’s properties. Measures of central tendency (mean, median, mode) and variability (range, standard deviation, interquartile range) summarize the data’s key attributes.
- Why it matters: Numerical summaries complement visualizations by quantifying patterns and making comparisons easier. For example, knowing the mean and standard deviation of a sales variable helps interpret its histogram.
- What to do: Use functions like
summary(),mean(),median(), andsd()to compute statistics. Pay attention to measures of spread, as they highlight variability and potential issues like skewness or extreme values.
Step 4: Detect Outliers with IQR, Z-Scores, or Visualizations
Outliers are data points that deviate significantly from the majority of values. Identifying them is critical because they can represent errors, unusual phenomena, or important insights.
- Why it matters: Outliers can distort statistical measures like mean and variance, affecting model accuracy and decision-making. At the same time, they may highlight rare but valuable cases, such as high-value customers or exceptional product performance.
- What to do: Apply statistical methods like the interquartile range (IQR) or Z-scores to detect outliers quantitatively. Use visualizations like box plots or scatter plots to confirm and understand these anomalies.
Step 5: Test for Skewness and Kurtosis
While visualizations and descriptive statistics provide initial insights, statistical tests for skewness and kurtosis offer a quantitative approach to understanding the shape of a distribution. These tests help determine whether the data is symmetric, leans to one side, or has heavy tails and extreme values. Such insights are essential for choosing the right modeling techniques and making data-driven decisions.
Why it matters: Testing for skewness and kurtosis allows you to quantify asymmetry and tail behavior in a variable’s distribution. This is critical for identifying potential biases or risks in the data, as well as determining whether assumptions of normality for certain statistical models are violated.
What to do: Use statistical measures and hypothesis tests to evaluate skewness and kurtosis. These tests will help determine if the variable significantly deviates from symmetry or normal tail behavior.
27.8 Conclusion
Univariate analysis provides the initial, crucial insights that business leaders need. Each of these concepts—mean, median, standard deviation, skewness, and outliers—contributes to more informed decision-making. Whether setting realistic sales targets, evaluating customer demographics, or pricing products, univariate insights offer the clarity needed to make effective choices. EDA matters for practical reasons:
Detect Data Quality Issues: Identify and address missing values, duplicates, and outliers to ensure the integrity and reliability of your dataset. These issues, if unchecked, can distort analysis and lead to inaccurate conclusions.
Understand Distributions Using Visual and Numerical Tools: Visualizations like histograms and box plots give an intuitive understanding of data patterns, while descriptive statistics quantify properties like central tendency and variability. Together, these tools provide a comprehensive view of each variable.
Effective Comparison and Interpretation: Descriptive statistics (mean, median, mode, variance) allow for quick data comparisons across different groups. In business analytics, this could mean understanding customer spending habits, employee performance across departments, or differences in product popularity.
Gain Foundational Insights for Deeper Analysis: By understanding individual variables, you establish a strong basis for exploring relationships between them. Insights gained during univariate EDA guide the development of hypotheses and inform subsequent modeling and decision-making.
Setting Benchmarks and Thresholds: In cases like quality control or risk analysis, knowing the natural variability in a data set lets you set realistic benchmarks. Identifying and analyzing the “normal” range helps to spot significant deviations, which might indicate issues or opportunities.
Anomaly Detection and Risk Identification: Abnormal distributions can indicate underlying risks or rare events that might skew typical results, such as a heavy-tailed distribution indicating potential risk in financial data. Identifying these traits early can guide more robust analyses that account for potential volatility or risk.
Customer Insights and Market Segmentation: In marketing analytics, for example, distribution patterns in customer demographics or purchase behaviors can reveal distinct market segments. Insights into the “shape” of this data help tailor products and campaigns to match customer profiles more closely.
Looking Ahead: As we move into bivariate analysis, where we examine relationships between two variables, these foundational skills will help us understand how different factors interact. For example, understanding individual distributions prepares us to explore questions like: “How does price relate to sales volume?” or “What is the relationship between customer age and spending behavior?”