22 Confidence Intervals and Hypothesis Testing

22.1 Drawing Conclusions from Data

In any data analysis, we often seek to understand the underlying truth of a population using data from a sample. While descriptive statistics summarize data, they don’t tell us how well the data represents the population. Statistical inference bridges this gap, allowing us to draw conclusions about the population based on sample data.

The Liberty Ships Dataset: Population vs. Sample

The Liberty ships dataset, introduced in Section 18.2, provides production data for ships built during World War II. While it contains all ships built by each shipyard (population data within shipyards), it includes only 8 of the 18 shipyards that contributed to Liberty ship production. This means:

Population Data: At the level of individual shipyards, we have complete data for all ships produced.
Sample Data: At the level of shipyards, we are working with a sample of the full population of 18 shipyards.

This distinction mirrors common challenges in data analysis:

Within each shipyard, we can compute population statistics, such as the mean and variance for production times or costs, with complete certainty.
Across shipyards, we must infer population parameters (e.g., the average production time across all shipyards) using sample statistics from our subset of shipyards.

The Challenge of Sampling

If we had data from all 18 shipyards, we could compute the true population mean and variance for production times and costs. However, with data from only 8 shipyards, we must use statistical inference to estimate these population parameters:

How close is the sample mean (from 8 shipyards) to the population mean (from 18 shipyards)?
How much variability exists in our sample statistics due to the selection of shipyards?

These questions highlight the role of confidence intervals and hypothesis testing in quantifying and addressing the uncertainty of sampling.

Connecting Samples to Populations

To estimate population parameters and test hypotheses based on our sample, we rely on:

Confidence Intervals:
- Provide a range of plausible values for a population parameter (e.g., the mean production time across all 18 shipyards).
- Reflect the uncertainty due to sampling variability.
Hypothesis Testing:
- Tests specific claims or assumptions about the population (e.g., whether the average production time differs between shipyards).

Using the Liberty Ships dataset, we’ll explore these tools in the context of real-world questions:

What is the range of plausible values for the average production time across all shipyards?
Do production costs vary significantly between shipyards?

These techniques help bridge the gap between the sample (our subset of shipyards) and the population (all shipyards), enabling us to draw meaningful conclusions despite incomplete data.

In this chapter, you’ll learn to:

Calculate confidence intervals for means.
Conduct basic hypothesis tests, including t-tests of differences in means.
Interpret results in an entrepreneurial context.

These skills will help you move from observing patterns to testing ideas and making data-driven decisions.

22.2 Demonstration Data

We’ll continue using the Liberty ships dataset from Section 18.2 to demonstrate confidence intervals and hypothesis testing. Specifically, we’ll examine:

Whether the average Total_Production_Days to build a ship differs significantly from historical benchmarks.
How Total_Cost varies between different shipyards.

This data provides a practical context for understanding how statistical inferences inform operational and strategic decisions.

# A tibble: 1,571 × 6
    Unit Yard        Way Direct_Hours Total_Production_Days Total_Cost
   <dbl> <chr>     <dbl>        <dbl>                 <dbl>      <dbl>
 1     1 Bethlehem     1       870870                   244   2615849 
 2     2 Bethlehem     2       831745                   249   2545125 
 3     3 Bethlehem     3       788406                   222   2466811 
 4     4 Bethlehem     4       758934                   233   2414978 
 5     5 Bethlehem     5       735197                   220   2390643 
 6     6 Bethlehem     6       710342                   227   2345051 
 7     8 Bethlehem     8       668785                   217   2254490 
 8     9 Bethlehem     9       675662                   196   2139564.
 9    10 Bethlehem    10       652911                   211   2221499.
10    11 Bethlehem    11       603625                   229   2217642.
# ℹ 1,561 more rows

22.3 Confidence Intervals

A confidence interval provides a range of plausible values for a population parameter based on a sample statistic. For example, if we want to estimate the population mean of a variable, we calculate the sample mean and then construct a confidence interval around it.

The width of the confidence interval reflects the uncertainty of the estimate:
- A narrow confidence interval suggests the sample statistic is a precise estimate of the population parameter.
- A wide confidence interval indicates greater uncertainty in the estimate.

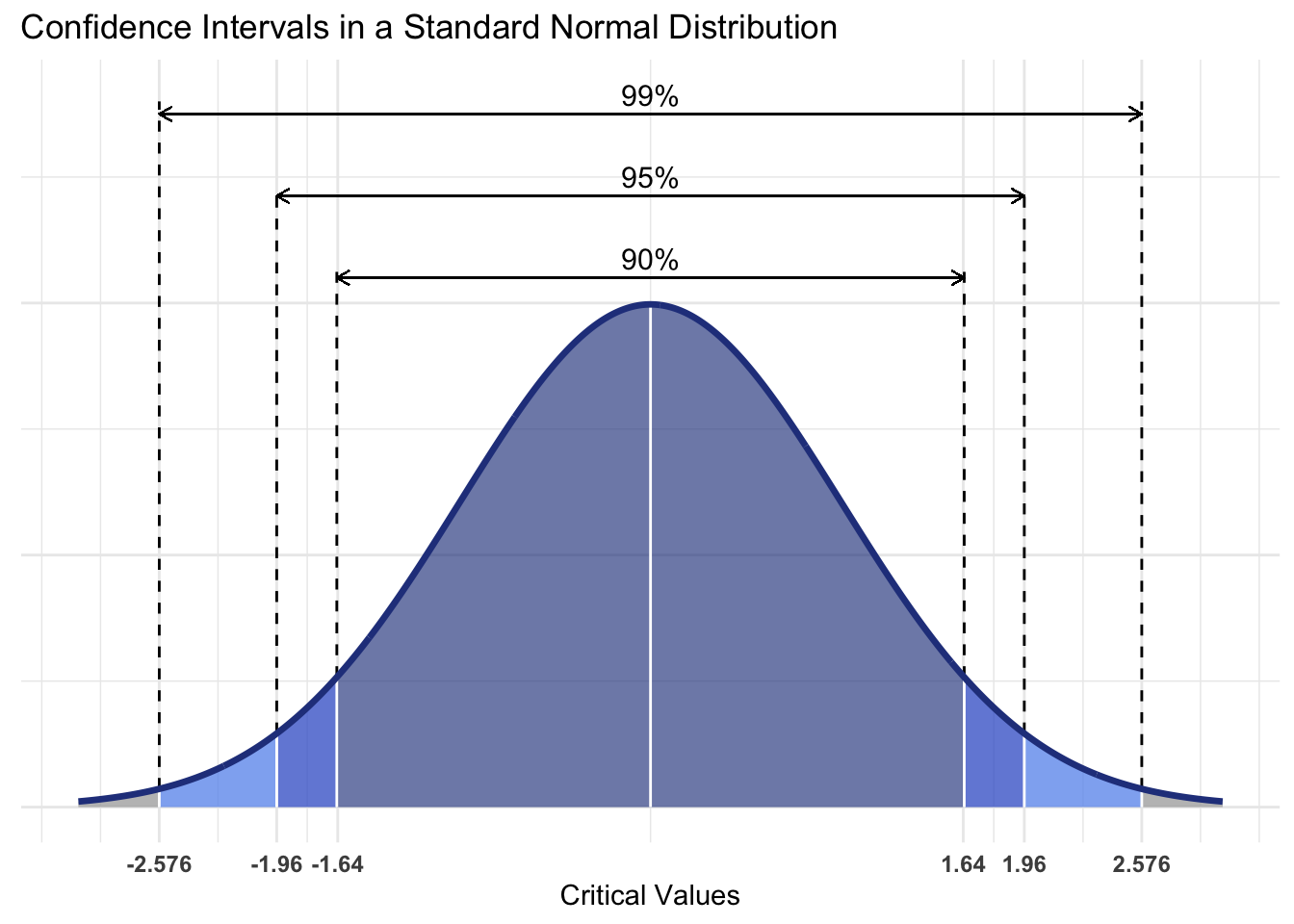
Figure 22.1: Confidence intervals as the probability that the population mean is between key critical values

Confidence Levels and Critical Values

In Figure 22.1, we visualize confidence intervals for commonly chosen confidence levels (90%, 95%, and 99%). Each interval highlights the critical values that define its boundaries.

A confidence level (e.g., 90%, 95%, 99%) represents the degree of certainty that a population parameter lies within the confidence interval. For example, a 95% confidence level means that if we repeated the sampling process 100 times, approximately 95 of those intervals would contain the true population mean.

The critical value is the point on the distribution corresponding to the chosen confidence level. For a standard normal distribution:

90% confidence level: Critical value ±1.645 (10% outside, 5% in each tail).
95% confidence level: Critical value ±1.96 (5% outside, 2.5% in each tail).
99% confidence level: Critical value ±2.576 (1% outside, 0.5% in each tail).

Conversely, these critical values define the confidence interval:

90% confidence interval: [-1.645, 1.645]
95% confidence interval: [-1.96, 1.96]
99% confidence interval: [-2.576, 2.576]

Why This Matters

Critical values and confidence levels enable us to calculate confidence intervals that quantify the uncertainty in our sample estimate. These intervals provide a range of plausible values for the population parameter, balancing:

Precision: Narrower intervals give more precise estimates.
Confidence: Higher levels of certainty (e.g., 99%) expand the interval.

The choice of confidence level depends on the context:

90% confidence: Suitable for exploratory analyses or where some uncertainty is acceptable.
95% confidence: The most commonly used standard for general analysis.
99% confidence: Applied in fields where high certainty is critical, such as medicine or quality control.

Calculating Confidence Intervals in R

We can calculate a confidence interval for the mean Total_Production_Days using R:

# Calculate confidence interval for mean Total_Production_Days
ci_days <- liberty_ship_data |>
  summarize(
    mean_days = mean(Total_Production_Days, na.rm = TRUE),
    ci_lower = mean_days - qt(0.975, df = n() - 1) * sd(Total_Production_Days, na.rm = TRUE) / sqrt(n()),
    ci_upper = mean_days + qt(0.975, df = n() - 1) * sd(Total_Production_Days, na.rm = TRUE) / sqrt(n())
  )

ci_days

# A tibble: 1 × 3
  mean_days ci_lower ci_upper
      <dbl>    <dbl>    <dbl>
1      64.5     62.2     66.7

Visualizing Confidence Intervals

Confidence intervals can be visualized using error bars to represent the range of uncertainty around the mean.

Visualizing Confidence Intervals for Total Production Costs by Yard

# Example of visualizing confidence intervals
liberty_ship_data |>
  group_by(Yard) |>
  summarize(
    mean_cost = mean(Total_Cost, na.rm = TRUE),
    ci_lower_cost = mean_cost - qt(0.975, df = n() - 1) * sd(Total_Cost, na.rm = TRUE) / sqrt(n()),
    ci_upper_cost = mean_cost + qt(0.975, df = n() - 1) * sd(Total_Cost, na.rm = TRUE) / sqrt(n())
  ) |>
  ggplot(aes(x = Yard, y = mean_cost, ymin = ci_lower_cost, ymax = ci_upper_cost, color = Yard)) +
  geom_pointrange() +
  labs(title = "Confidence Intervals for Average Total Cost by Yard", y = "Average Cost", x = "Shipyard") +
  scale_y_continuous(labels = scales::dollar_format()) + 
  theme_minimal()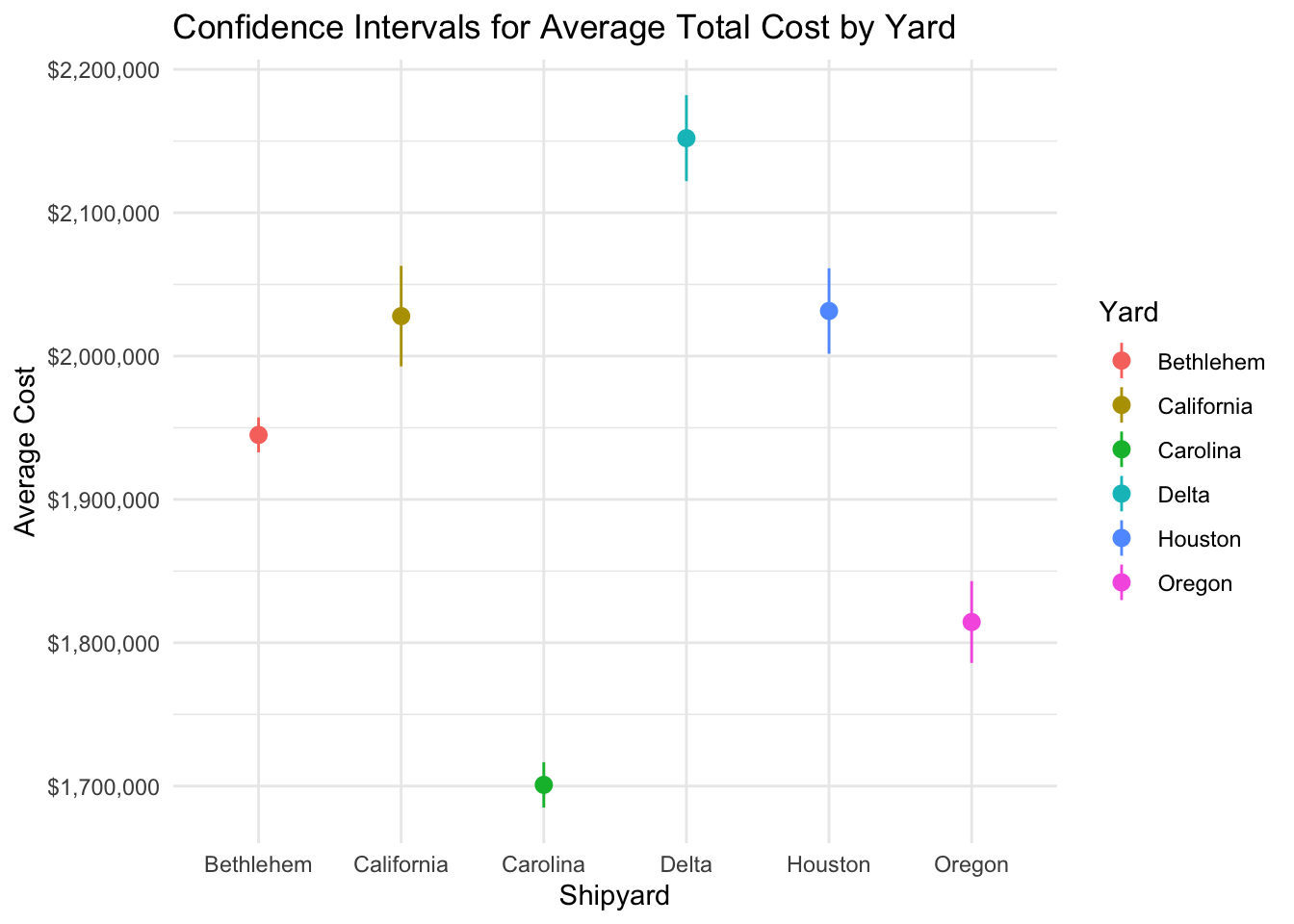

Figure 22.2: 95% confidence intervals for average production cost for each shipyard

Estimating the Mean Production Time

Suppose we calculate a 95% confidence interval for Total_Production_Days as [62.19, 66.72]. This means we are 95% confident the true average production time for Liberty Ships lies between 62.19 and 66.72 days.

Critical values (z-scores or t-scores) define the boundaries of confidence intervals, connecting our chosen confidence level (e.g., 95%) to the statistical distribution of the data.

22.4 Hypothesis Testing

While confidence intervals help estimate parameters, hypothesis testing enables us to evaluate specific claims about the population. This involves:

Null Hypothesis (\(\mathsf{H_0}\)): The baseline assumption (e.g., no difference or effect).
Alternative Hypothesis (\(\mathsf{H_a}\)): The claim we want to test (e.g., there is a difference between groups).
Significance Level (\(\alpha\)): The threshold for rejecting \(\mathsf{H_0}\), commonly set at 0.05.

Testing Average Production Time with a t-Test

A t-test compares means to determine if differences are statistically significant. Here’s an example testing whether the average Total_Production_Days differs from 100:

\(\mathsf{H_0}\): Total_Production_Days = 100
\(\mathsf{H_a}\): Total_Production_Days \(\mathsf{\ne}\) 100

One-Sample t-Test

# One-sample t-test for Total_Production_Days
library(broom)
t_test_result <- t.test(
  liberty_ship_data$Total_Production_Days,
  mu = 100,
  alternative = "two.sided",
  conf.level = 0.95
)

# Extract confidence interval values
#t_test_tidy <- tidy(t_test_result)
#conf_low <- round(t_test_tidy$conf.low, 2)
#conf_high <- round(t_test_tidy$conf.high, 2)
t_test_result


    One Sample t-test

data:  liberty_ship_data$Total_Production_Days
t = -29.52, df = 1448, p-value < 2.2e-16
alternative hypothesis: true mean is not equal to 100
95 percent confidence interval:
 62.09428 66.81808
sample estimates:
mean of x 
 64.45618

Interpreting Results

p-Value:
- The probability of observing the data if \(\mathsf{H_0}\) is true.
- A small p-value (e.g., p < 0.05) suggests the data is unlikely under \(\mathsf{H_0}\), leading to its rejection.
- In the case of Total_Production_Days, the p-value is effectively 0, indicating that we can reject \(\mathsf{H_0}\) at the 1% significance level and suggesting the mean production time differs from 100 days.
Confidence Interval:
- Provides the range of plausible values for the true mean.
- If the confidence interval does not include the hypothesized value (e.g., 100), we reject \(\mathsf{H_0}\).
- In the case of Total_Production_Days, the confidence interval is [62.09, 66.82] which does not contain 100, i.e., 100 days is not a plausible value for average production days.
Effect Size:
- While statistical significance answers whether a difference exists, effect size quantifies the magnitude of that difference.
- Reporting effect sizes ensures practical significance is considered alongside statistical results.

Drawing a Conclusion

Given that the p-value is effectively 0 and the confidence interval for the mean production time is [62.09, 66.82], we conclude:

The average production time is significantly different from 100 days.
The range of plausible values (62.09 to 66.82 days) provides additional context for our confidence about this difference.

Testing Average Production Time by Visualizing Confidence Intervals by Yard

# Example of visualizing confidence intervals
overall_mean <- mean(liberty_ship_data$Total_Production_Days, na.rm = TRUE)

liberty_ship_data |>
  group_by(Yard) |>
  summarize(
    mean_days = mean(Total_Production_Days, na.rm = TRUE),
    ci_lower_days = mean_days - 
      qt(0.975, df = n() - 1) * sd(Total_Production_Days, na.rm = TRUE) / sqrt(n()),
    ci_upper_days = mean_days + 
      qt(0.975, df = n() - 1) * sd(Total_Production_Days, na.rm = TRUE) / sqrt(n())
  ) |>
  ggplot(aes(x = Yard, y = mean_days, ymin = ci_lower_days, ymax = ci_upper_days)) +
  geom_pointrange(aes(color = Yard)) +
  geom_hline(yintercept = overall_mean, linetype = "dashed", color = "darkgray", linewidth = 0.8) +
  annotate("text", x = 1, y = overall_mean + 2, label = paste0("Overall mean: ", round(overall_mean, 2)), color = "darkgray", hjust = 0) +
  labs(title = "Confidence Intervals for Average Total Production Days by Yard", 
       y = "Average Days in Production", 
       x = "Shipyard") +
  theme_minimal()

Figure 22.3: Visualizing confidence intervals as a difference-in-means test

Drawing a Conclusion

The overall mean for production days across all shipyards is 64.46 days. Visual inspection shows that the 95% confidence interval for Bethlehem’s production days does not overlap this mean, suggesting a significant difference.

This conclusion is confirmed by calculating Bethlehem’s confidence interval as [50.04, 57.76], which does not include the overall mean.

With 95% confidence, we conclude that average production days at the Bethlehem yard differ from the average across all shipyards.

22.5 Practical Tips for Drawing Conclusions

Avoid Overinterpreting p-Values: A small p-value indicates statistical significance, but practical relevance depends on the effect size and context.
Report Confidence Intervals: Confidence intervals complement p-values by providing a range of plausible values for the parameter of interest.
Check Assumptions: Ensure the assumptions of the t-test (e.g., normality, independence) are met.
Use Visualizations: Graphs, such as boxplots or density plots, can illustrate differences and enhance interpretation.

22.6 Conclusion: From Data to Decisions

Confidence intervals and hypothesis testing form the backbone of statistical inference, helping us draw conclusions and assess uncertainty about population parameters. By combining these tools:

Confidence intervals quantify the precision and reliability of estimates.
Hypothesis testing evaluates claims about populations and assesses statistical significance.

Together, they enable us to make informed decisions and communicate findings clearly, balancing statistical rigor with practical relevance. They validate assumptions and guide actions based on evidence. In the next chapter, we’ll explore how to make decisions under uncertainty using statistical decision rules.